Which Is Greater?
Geometry
Level
1
Which region is larger, blue or red?
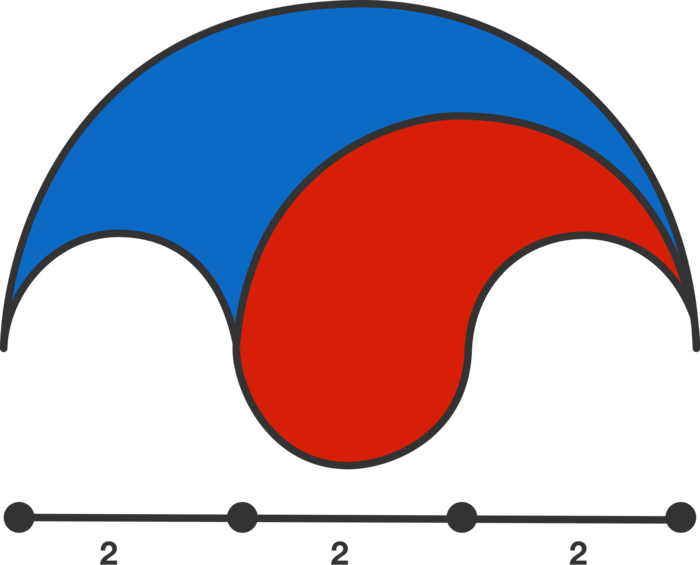
Blue
Red
They have the same area
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Adding a line to this image makes it easier to see its parts.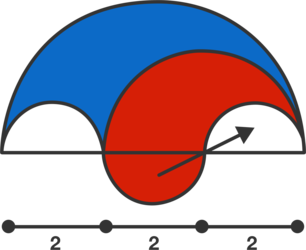
The two red parts combine to make a semi-circle with a radius of 2 and an area of 2 1 π ( 2 ) 2 = 2 π .
The area of the entire figure is the area of a semi-circle with a radius of 3 minus the area of a semi-circle with a radius of 1: 2 1 π ( 3 ) 2 − 2 1 π ( 1 ) 2 = 4 π .
If the area of the figure is 4 π , and the area of the region shaded red is 2 π , then the area of the region shaded blue must also be 2 π . The areas of the red and blue regions are equal.