Geometry problem #133126
What is the sum of the angles numbered 1-8?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
7 solutions
The sum of the exterior angles of a polygon is.... NOT 360º
it's:
(N-2)*180
(you meant quadrilateral and wrote polygon...)
Log in to reply
(N-2)*180 is the sum of the interior angles of a polygon.
Imagine it as a square 90*8=720 Simple
Relevant wiki: General Polygons - Angles
The total sum of degrees of all four vertices is 4 ⋅ 3 6 0 ° = 1 4 4 0 ° . The sum of the internal angles of a quadrilateral is 360°, and as their vertical angles are equal to them, their sum is also 360°. The only angles we haven't counted are the angles numbered 1-8, So their sum is:
(total angles of 4 vertices)-(quadrilateral internal angles)-(vertical angles to quadrilateral internal angles)= 4 ⋅ 3 6 0 ° − 3 6 0 ° − 3 6 0 ° = 2 ⋅ 3 6 0 ° = 7 2 0 ° .
▄
I barely remember this from middle school in Abu Dhabi-UAE where all science is mandatory.
Log in to reply
I'm right there with you. I am borderline torturing myself but I have decided that I need to learn it. I struggle with it and want to get better 😁
Moderator note:
Let's take a math competition perspective on this answer:
In a competition that requires answering problems via a proof, this answer would not be acceptable, because it proved a specific case and not the general one the problem asks for. (Note that for Brilliant.org solutions, in general we request for full proofs.)
In a competition that only requires an answer (especially one where the answer is needed quite rapidly), this sort of technique of assuming the uniqueness of an answer can be useful. Here's another problem (from a Martin Gardner book) where a similar technique works:
A six inch high cylindrical hole is drilled through the center of a sphere. How much volume is left in the sphere?
If you make the sphere have a radius of 3 inches, the "hole" has a radius of 0. Applying the volume of a sphere formula 3 4 π r 3 , the volume "remaining" is 3 6 π cubic inches.
The angles may not be 90° You have to prove it generally
Log in to reply
Not if you're doing a multiple choice question. This answer shows that 720 is the only possible solution of the answers given. There's nothing in the problem that says the quadrilateral isn't a rectangle. Therefore any general solution must also hold in that particular case. And this is a case that is rather easy to solve.
Log in to reply
While this is a successful method for getting a correct multiple choice answer, it does not make it a correct proof. (This is similar to our problems which ask for the maximum or minimum way to do something and people produce an example as the "answer" - but they have to prove there is no larger / smaller value to be complete.)
As only one of the possible answers can be true and there are no angles given in the question to start with, we must assume that one of the possible answers must be true for any four lines in similar arrangement. Therefore summing up the 90° angles in a perpendicular arrangement of lines leads to the correct sum.
@Calvin Lin While it is true that this technique does not provide a proof, it is actually a worthwhile problem solving strategy. If you have no idea of what the problem is like, it is a good idea to play around and try the limiting cases.
Log in to reply
Yep, and it's certainly good to have know the answer before you start the proof than work entirely open-ended.
Log in to reply
I am in agreement.
Sometimes I feel an urge to respond to the challenge master's note...
I like this approach but in this case it is better to stretch the quadrilateral. It it becomes apparent that 4 of the angles are a bit less than 180 and 4 are a bit more than 0.
that's very easy to think.
as there are 4 vertices, total summation of angle is = 3 6 0 × 4 = 1 4 4 0 degrees
now, there is a quadrilateral which has total 360 degrees(which has not been counted) and its vertical angles are equal.
so, total 3 6 0 × 2 = 7 2 0 degrees has not been counted.
so, there remains= 1 4 4 0 − 7 2 0 = 7 2 0 degrees.(that has been wanted) ,
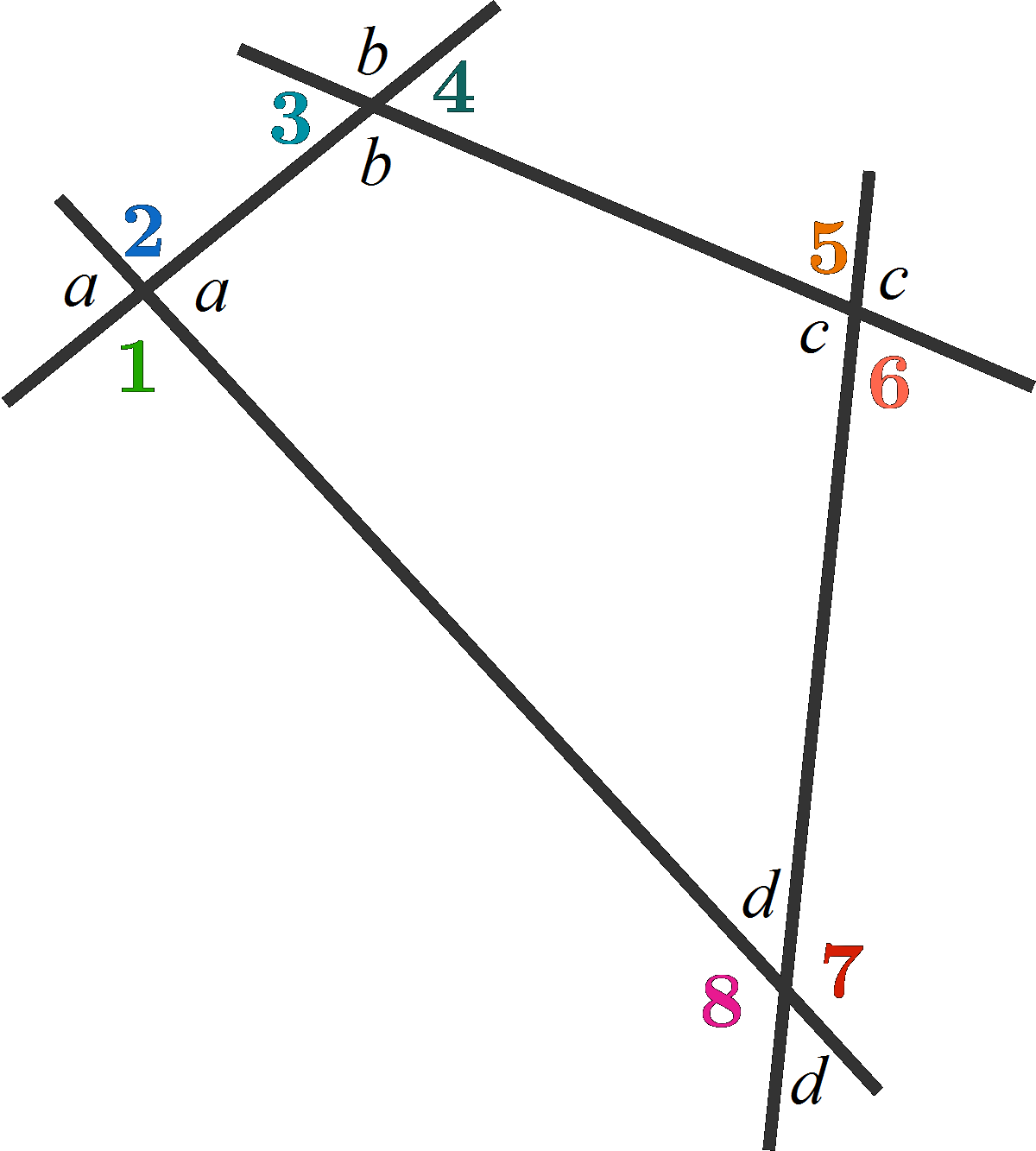
Let the unmarked opposite angles be a , b , c , and d as shown in the figure. We note that each point (intersection of two straight lines) is 3 6 0 ∘ and the sum of angles numbered 1-8 is given by:
k = 1 ∑ 8 ∠ k + 2 ( a + b + c + d ) k = 1 ∑ 8 ∠ k + 2 × 3 6 0 ∘ ⟹ k = 1 ∑ 8 ∠ k = 4 points 4 × 3 6 0 ∘ = 4 × 3 6 0 ∘ = 7 2 0 ∘ Note that a , b , c , d , are the 4 quadrilateral internal angles.
The logic I used was the fact that each intersection equated to 360°, therefore two of the angles must be equal to 180°. So...
4*180=720
*two angless on opposite sides
I used almost the same as that, but that four angles equal 360, so 360 times 2 as there are 8 angles.

Relevant wiki: General Polygons - Angles