Geometry problem #133132
The area of the large square is 100 and all of the small, blue squares are congruent.
What is the total area shaded blue?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
15 solutions
@József Inczefi Thanks for clarifying. I looked into the history and agree with your interpretation.
Sorry for jumping to conclusions on the surface.
I counted the blue square which was 25, and then I counted the white triangles (four, one from each corner) and white squares and found they also totaled to 25 so then I knew the answer was 50.
an other reason why I got that wrong is because I d'ont know what congurent means... do you?
Log in to reply
Brilliant itself has tons of wikis for you to look up, here you go :)
I think i misunderstood the meaning congurent means so I just assumed the answer
I see that but the outer edge of the square has white triangles & there are no blue triangles.
Log in to reply
If you check the small red square the pattern you will get how it is calculated
Does the triangles make up for only 4 in each row of white squares while each row of blue there are 5?
Yes it does count white the same. Mmm ok
Relevant wiki: Length and Area - Composite Figures
look carefully,
there is 25 blue squares....(easily countable)
and there is also 25 white squares..[16 full squares,.............................16 half squares(in top of every side)=8 full squares,...........and 4 quarter square in corners make a full
square;total=25squares]
now, total area=100
.............total squares=50 and blue squares=25
so, blue squares cover 2 1 of the area or the area of blue squares is=50
I thought the same form to count the area.
Thou it looks so difficult to guess what its answer would be but, looking at it carefully well, you've gotten its solution.
Jtcsdc12 I had forgotten what congruent meant, but correctly soved by inspection.
This was pretty challenging. I had my dad helping me, we got the counting of the white spaces wrong wich also made our answer wrong.
Log in to reply
i think that is not so challenging to count.
at first count the full squares,then half squares, then corners.[they all are in a pattern]
if need any other help,just let me know.
yes yes WE KNOW YOU DUMMY! ):O
Log in to reply
didn't understand.
Please be respectful to other Brilliant users in the comments.
The answer is
50
. Notice that the large square has sides of length 10, which is the same as the length of 5 times the diagonal length of the blue square, based on the figure.
So, one can directly solve for the side length of the blue square.
1
0
=
5
l
2
⇒
l
=
2
/
2
=
2
. This gives an area of
2
for a single blue square. Since there are 25 total squares the total area is
2
5
×
2
=
5
0
.
If the area of the big square is 100, then it's height is 10. Looking at the figure, we see that 5 times the length of the diagonal of a blue square equals 10. Therefore, the length of the diagonal is 2. From this, we deduce that the length of the side of a blue square is 2 . Therefore, the total area of the blue squares is 2 5 × 2 × 2 = 50
Can someone explain to [email protected]
Why is it 25.√2.√2
prop not clear.Not able to understand
The area covered by white squares= The area covered by blue squares So area covered by blue squares=100/2=50 sq. units
Since the side lengths are 10, and there are 5 squares connected at the vertices for each side, the diagonal of each blue square is 2. From that info, the side lengths of the blue squares are 2^1/2, and the area is 2. 2×25=50
A rather lengthy solution would be this one:
We know that the side of the big triangle is 10, for 10^2 = 100. Let's call 1/10 of this side "x" = 1. Two "x" form a right triangle with the side of a blue square "y" (see the top right corner).
Since a^2 + b^2 = c^2, that means that x^2 + x^2 = y^2 = 2, the squared side of a blue square. Squaring the side of a blue square naturally gives its area, in this case it must be 2.
Now the total area is 100, there are 25 blue squares, so their area covers half the area of the big square, which is 50.
On a side note: this means that the side of a blue triangle is actually the square root of 2, an irrational number.
I agree with geoff philling. I solved it the same way. The four small triangles in four corners add up to form 1 square.Also the medium sized triangles on each side of the bigger square are taken in pairs to form 1 square each.Also since each blue square is equal in area so the small white square surrounded by 4 blue squares is equal to the area of 1 blue square. Using these rules we get that there are total 50 equal squares forming the big square. This means area of 50 squares = 100. Area of 1 square= 2. No. Of blue squares= 25 Area of blue squares= 25 × 2= 50.
I feel like a complete moron for using trigonometry to solve this. I focused on finding the area of one blue square instead of the bigger picture. Oh well, it was fun ;3
The number of white squares is equal to the number of blue squares across rows and columns = 5. Consequently, blue squares would occupy half the area
There are 50squares each of two unit area Extending this logic there are half blue squares there fore 100/2=50
count the blue diamond and multiply by 2
Shift all the blue square in the white region...u got the answer
each square is the sum of two rt triangles thus by Pythagorean theorem the side of each square is sqr 2. this implies the area of each square is 2. so 2 x 25 = 50
I twisted the blue boxes in my mind, and a checker board was left. So, I went with my mathematical gut.
I used trigonometry to solve it lmao
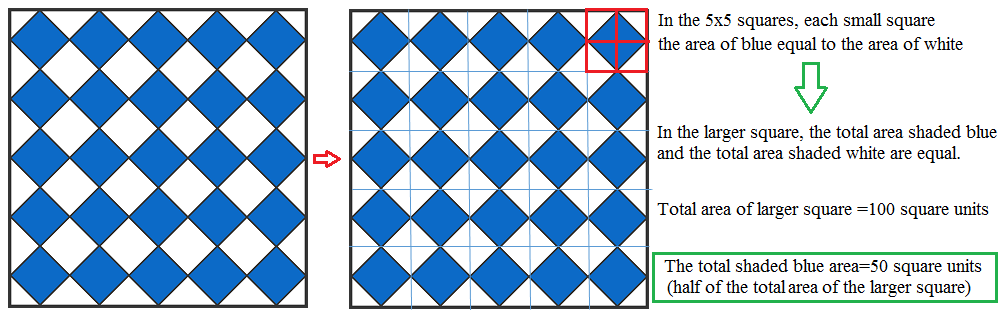
The above picture is made up of loads of little squares like the one shown in the top right in red:
Each is half blue. Therefore the area of the blue region of the entire square is half of its area or 5 0