Geometry Problem
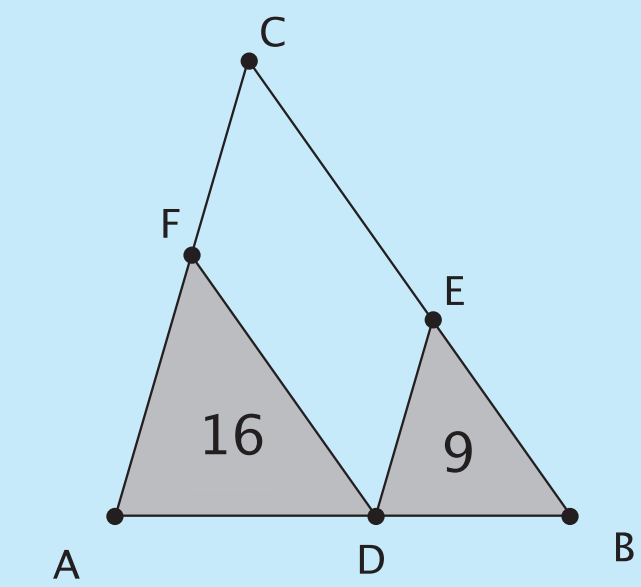 In image above the lines
D
E
and
D
F
are parallel to sides
A
C
and
B
C
of the triangle
A
B
C
The triangles
A
D
F
and
D
B
E
are triangles with area
1
6
and
9
respectively. What is the area of
C
F
D
E
?
In image above the lines
D
E
and
D
F
are parallel to sides
A
C
and
B
C
of the triangle
A
B
C
The triangles
A
D
F
and
D
B
E
are triangles with area
1
6
and
9
respectively. What is the area of
C
F
D
E
?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
G E N I U S
Firstly, denote CF = ED = y , DF = CE = x and ∠ CFD = θ . Now note that in terms of scale factor: Δ A F D = 3 4 Δ D B E ⇒ y = 4 3 A F a n d x = 3 4 E B . This means that if we draw line CD then area [CFDE] = x y s i n θ (1). Now finding the area of Δ DBE (using 2 1 AB sin θ = A T again ): 9 = 8 3 ( E B ) . ( A F ) s i n ( 1 8 0 − θ ) = 8 3 × 4 3 x × 3 4 y s i n θ = 8 3 x y s i n θ ∴ ( f r o m ( 1 ) ) a r e a ( C F E D ) = 9 × 3 8 = 2 4
CF // DE, and FD//CE, then FDEF is a parallelogram. The ratio of AD to DE is 4:3.Let the area of [CDF] =x , [CDE]=x.So the area ratio of [ADC]/[CDB] =(x+16)/(x+9) = 4/3, then x=12. So the area of CFDE = 2(12) = 24.
My approach is same of Niranjan Khanderia, ..people in same age range frequently have coincident views.
△ s A F D a n d D E B a r e s i m i l a r ∵ o f ∥ l i n e s . S i d e s o f s i m i l a r △ s a r e p r o p o r t i o n a l t o t h e i r a r e a s . ∴ A D : D B : : 4 : 3 . S o A D : A B : : 4 : 7 ⟹ a r e a s A D F : A B C : : 4 2 : 7 2 i m p l i e s a r e a A B C = 4 9 A r e a s C F D E = A B C − A D F − D B E = 4 9 − 1 6 − 9 = 2 4 2 4