Geometry problem #2
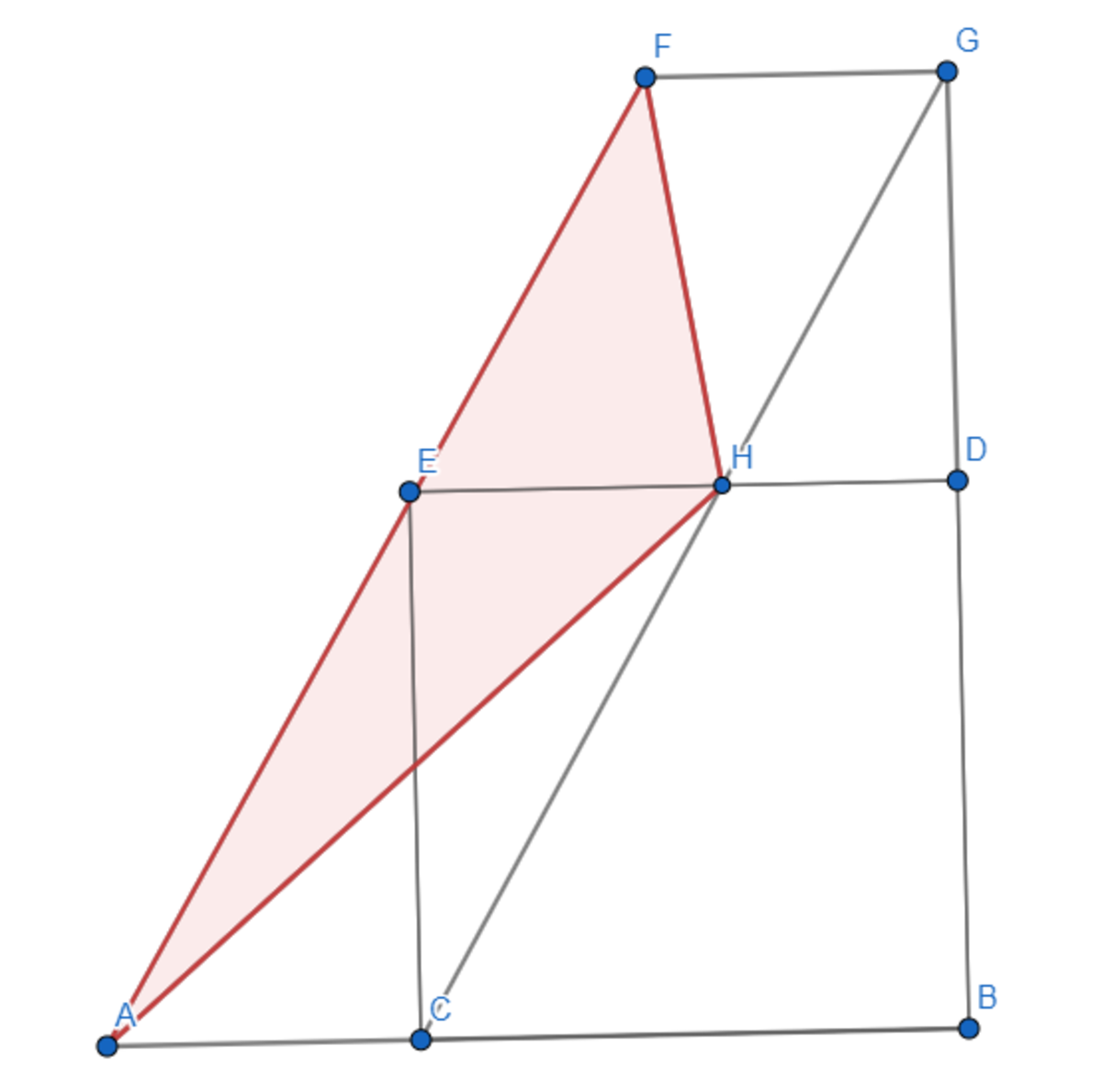
In the image below, B C E D is a square and A C G F is a parallelogram. B D G and A C B are straight lines. If B E = 8 2 , find the area of △ A F H .
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
 In the animation, every moving triangle preserves its area, because the varying vertex moves parallel to the opposite highlighted base. Hence, the area of
△
A
F
H
equals half the area of the square
B
C
E
D
. But,
[
B
C
E
D
]
=
2
1
B
E
2
.
Hence,
[
A
F
H
]
=
2
1
[
B
C
E
D
]
=
2
1
×
2
1
×
(
8
2
)
2
=
3
2
In the animation, every moving triangle preserves its area, because the varying vertex moves parallel to the opposite highlighted base. Hence, the area of
△
A
F
H
equals half the area of the square
B
C
E
D
. But,
[
B
C
E
D
]
=
2
1
B
E
2
.
Hence,
[
A
F
H
]
=
2
1
[
B
C
E
D
]
=
2
1
×
2
1
×
(
8
2
)
2
=
3
2