A Funky Yin Yang
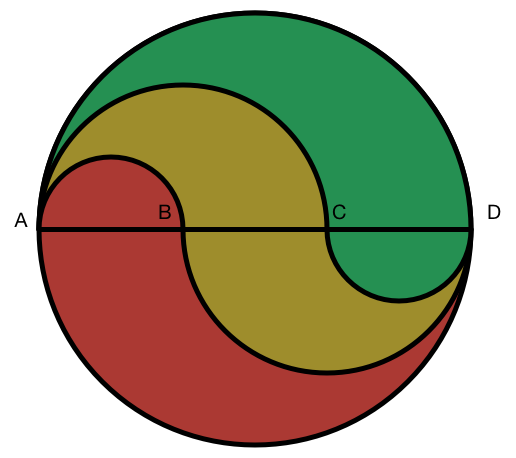 are equally spaced points on a line. Semicircles are constructed on both sides, and colored in, as in the above image.
are equally spaced points on a line. Semicircles are constructed on both sides, and colored in, as in the above image.
Which region is the smallest?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The regions all have the same area! We will show this by calculating the individual area of each colored region. For the ease of calculation, let's assume that the distances are A B = B C = C D = 2 .
Red region: ( π × 1 2 ) + ( ( π × 3 2 ) − ( π × 2 2 ) ) = 6 π .
Yellow region: ( ( π × 2 2 ) − ( π × 1 2 ) ) + ( ( π × 2 2 ) − ( π × 1 2 ) ) = 6 π .
Green region: ( ( π × 3 2 ) − ( π × 2 2 ) ) + ( π × 1 2 ) = 6 π .