Bridge Over...Semicircle

$\tan 30=\dfrac{28}{x}$

$\dfrac{\sqrt{3}}{3}=\dfrac{28}{x}$

$x=\dfrac{84}{\sqrt{3}}$

Rationalize the denominator by multiplying the right side by $\dfrac{\sqrt{3}}{\sqrt{3}}$

$x=\dfrac{84}{\sqrt{3}} \times \dfrac{\sqrt{3}}{\sqrt{3}}=\dfrac{84\sqrt{3}}{3}=$ $\boxed{28\sqrt{3}}$

Note:

$\dfrac{\sqrt{3}}{\sqrt{3}}=1$ so the value of $x$ was not changed.

51751s

Observe that triangle $ABO$ is a right triangle with $\angle ABO=90^\circ$ and $\angle BAO=30^\circ.$ Then since the length of $\overline{OB}$ is given as $28$ inches, the length of $\overline{AB}$ is $\tan60^\circ\times\overline{OB}=28\sqrt{3}$ inches.

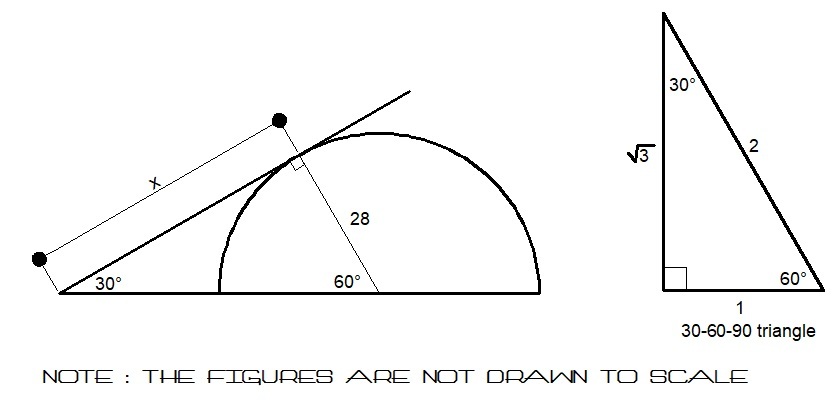
By ratio and proportion using the $30-60-90$ right triangle, we have

$\dfrac{x}{\sqrt{3}}=\dfrac{28}{1}$

$x=28\sqrt{3}$