Geometry problem by Kevin Tran (2)

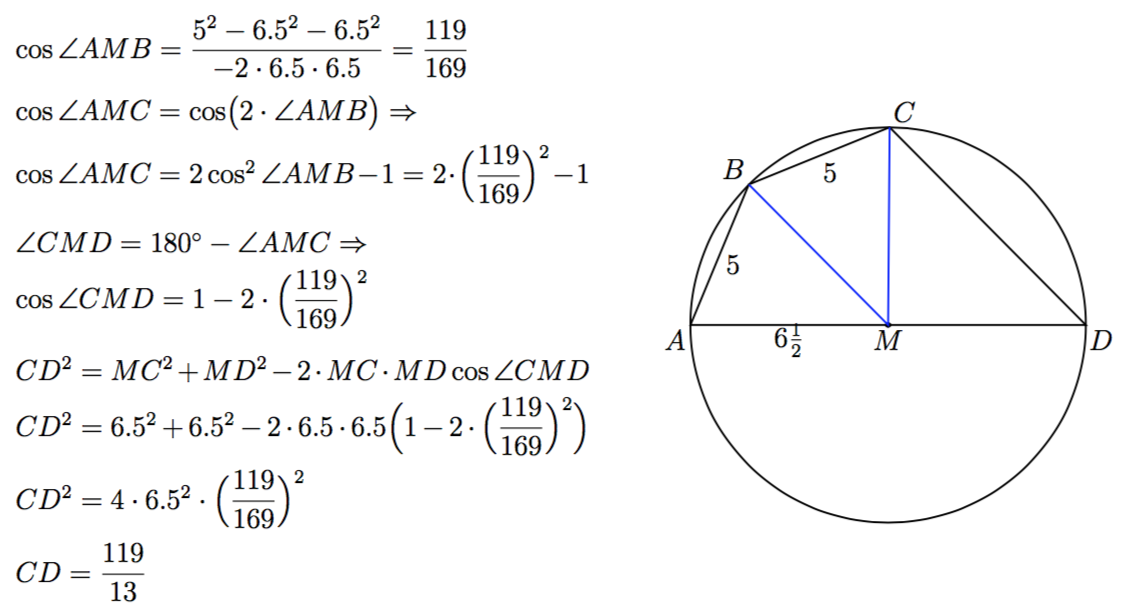
Generally speaking, if a chord of a circle spans angle $2\theta$ , then its length is $2r\sin \theta = d\sin\theta$ .

Suppose that $AB = BC = x$ each span an angle $2\alpha$ , and $CD = y$ spans an angle $2\beta$ , and $2(2\alpha) + 2\beta = 180^\circ$ .

Then $y = d\sin\beta$ , $x = d\sin\alpha$ , and $\beta = 90^\circ - 2\alpha$ ; therefore $y = d\sin(90^\circ - 2\alpha) = d\cos 2\alpha = d(1 - 2\sin^2\alpha) = d\left(1 - 2\cdot\left(\frac x{d}\right)^2\right) = \frac{d^2 - 2x^2}{d}.$

In this case, $d = 13$ and $x = 5$ , so that $y = \frac{13^2 - 2\cdot 5^2} 13 = \frac{119}{13};$ the answer to the problem is $119 + 13 = \boxed{132}$ .