Geometry problem No.3

Let $h_1$ be the distance along the axis from the apex to the center of the upper base of the conical frustum.

The upper base radius is $r_1 = h_1 \tan \theta$

The lower base radius is $r_2 = \tan \theta (h_1 + 2 R )$

The difference in volume between the two cones with the two bases specified above is

$V_1 = \frac{1}{3} \pi r_2^2 (h_1 + 2 R) - \frac{1}{3} \pi r_1^2 h_1$

$= \frac{1}{3} \pi \tan^2 \theta ( (h_1 + 2 R)^3 - h_1^3 )$

$= \frac{1}{3} \pi \tan^2 \theta ( 6 h_1^2 R + 12 h_1 R^2 + 8 R^3 )$

$= \frac{2}{3} \pi R^3 \tan^2 \theta ( 3 (h_1/R)^2 + 6 (h_1/R) + 4 )$

We also have that the lateral (slant) height of the frustum is

$s = r_1 + r_2 = \sqrt{ (r_1 - r_2)^2 + (2 R)^2 }$

From which it follows that $r_1 r_2 = R^2$

but this means that $\tan^2 \theta (h_1^2 + 2 R h_1) = R^2$

therefore, $\tan^2 \theta ( (h_1/R)^2 + 2 (h_1/R) ) = 1$

Use this last equation in the expression for the volume:

$V_1 = \frac{2}{3} \pi R^3 ( 3 \tan^2 \theta ( (h_1/R)^2 + 2 (h_1/R) ) + 4 \tan^2 \theta) = \frac{2}{3} \pi R^3 ( 3 + 4 \tan^2 \theta)$

but this volume is twice the volume of the sphere, hence,

$\frac{1}{3} \pi R^3 (3 + 4 \tan^2 \theta ) = \frac{4}{3} \pi R^3$

thus, $3 + 4 \tan^2 \theta = 4$

so that, $\tan \theta = \dfrac{1}{2}$

therefore, $\tan \varphi = ( \dfrac{1}{2} )^{-1} = \boxed{2}$

Label the diagram as follows, where $E$ is the point of tangency between the sphere and the cone:

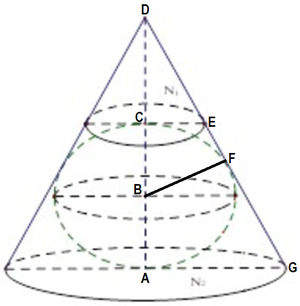
Let $CD = 1$ , $x = AC$ , $r = CE$ , and $R = AG$ , so that $AB = BC = BF = \frac{1}{2}x$ .

Since $\triangle BFD \sim \triangle GAD$ by AA similarity, $\cfrac{BF}{BD} = \cfrac{AG}{DG}$ , or $\cfrac{\frac{1}{2}x}{\frac{1}{2}x + 1} = \cfrac{R}{\sqrt{R^2 + (x + 1)^2}}$ , which rearranges to $R = \frac{1}{2}x\sqrt{x + 1}$ .

Since $V_S = \frac{1}{2}V_{N_2}$ , $\frac{4}{3}\pi BF^3 = \frac{1}{2}(\frac{1}{3}\pi \cdot AG^2 \cdot AD - \frac{1}{3}\pi \cdot CE^2 \cdot CD)$ , or $\frac{4}{3}\pi (\frac{1}{2}x)^3 = \frac{1}{2}(\frac{1}{3}\pi \cdot R^2 \cdot (x + 1) - \frac{1}{3}\pi \cdot r^2 \cdot 1)$ , or $x^3 = R^2(x + 1) - r^2$ .

Substituting $R = \frac{1}{2}x\sqrt{x + 1}$ into $x^3 = R^2(x + 1) - r^2$ gives $x^3 = (\frac{1}{2}x\sqrt{x + 1})^2(x + 1) - r^2$ , which rearranges to $r = \frac{1}{2}x(x - 1)$ .

Finally, since $\triangle BFD \sim \triangle ECD$ by AA similarity, $\cfrac{R}{x + 1} = \cfrac{r}{1}$ , or $\cfrac{\frac{1}{2}x\sqrt{x + 1}}{x + 1} = \cfrac{\frac{1}{2}x(x - 1)}{1}$ , which solves to $x = \cfrac{1 + \sqrt{5}}{2} = \phi$ (the golden ratio!)

Therefore, the tangent of the acute angle in the isosceles trapezoid is $t = \cfrac{AD}{AG} = \cfrac{CD}{CE} = \cfrac{1}{r} = \cfrac{1}{\frac{1}{2}x(x - 1)} = \cfrac{1}{\frac{1}{2}\phi(\phi - 1)} = \cfrac{1}{\frac{1}{2}\cdot 1} = \boxed{2}$ .

V(S) = V(N2) / 2
= 4πr³ / 3
V(N2) = 8πr³ / 3
= π[ (a² + 4[(a + b) / 2]² + b²) / 6 ] × [ 2r ]
= π(2a² + 2ab + 2b²)(2r) / 6
= π(a² + ab + b²)(2r) / 3
where a is the upper base radius and b is the lower base radius of N2.

(2r)² = a² + ab + b²

(Hypothenuse)² = (base leg)² + (height leg)²
(a + b)² = (b – a)² + (2r)²
a² + 2ab + b² = b² – 2ab + a² + (2r)²
(2r)² = 4ab
r² = ab

(b – a)² = b² – 2ab + a²
= (a² + ab + b²) – 3ab
= (2r)² – 3r²
= r²

Tan theta = (2r) / (b – a)
= 2r / r
= 2