Geometry problem - volume calculation
You have a sphere with center O and radius 5 , and a point A that is 1 3 units away from the center of the sphere. You construct the tangent cone to the sphere with apex at point A . Find the volume bounded by the lateral surface of the cone and the sphere. If the volume can be written as b a π for coprime integers a , b , find a + b .
The answer is 1639.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
In the cross section, we have the following situation,
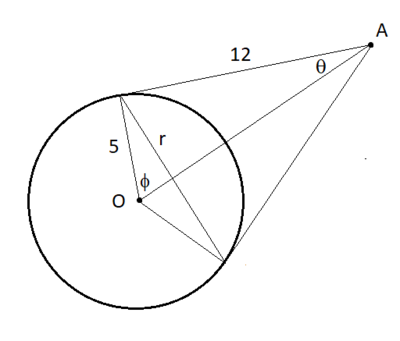
The semi-vertical angle of the cone is θ = tan − 1 ( 1 2 5 ) , therefore angle ϕ = 2 π − θ = tan − 1 ( 5 1 2 ) . The radius of the base of the cone is r = 5 sin ϕ = 1 2 sin θ = 1 3 6 0 .
The surface area of lateral surface of the cone is
S 1 = π r s = 1 3 6 0 ( 1 2 ) π = 1 3 7 2 0 π
and the surface area of the spherical cap is given by,
S 2 = 2 π ( 5 ) 2 ∫ 0 ϕ sin t d t = 5 0 π ( 1 − cos ϕ ) = 5 0 π ( 1 − 1 3 5 ) = 1 3 4 0 0 π
Hence, the volume contained between them is given by,
V = 3 1 ( 5 S 1 − 5 S 2 ) = 3 5 π ( 1 3 3 2 0 ) = 3 9 1 6 0 0 π
Therefore, the answer is 1 6 0 0 + 3 9 = 1 6 3 9 .
Label the cross-section as follows:
Then O B = O D = O E = 5 and O A = 1 3 , and by the Pythagorean Theorem on △ O B A , A B = A D = 1 2 .
Since △ O C B ∼ △ O B A by AA similarity, B C O C = A B O B , or B C O C = 1 2 5 , and by the Pythagorean Theorem on △ O C B , O C 2 + B C 2 = O B 2 or O C 2 + B C 2 = 2 5 . These equations solve to O C = 1 3 2 5 and B C = 1 3 6 0 . By segment addition, A C = A O − O C = 1 3 − 1 3 2 5 = 1 3 1 4 4 , and E C = O E − O C = 5 − 1 3 2 5 = 1 3 4 0 .
The desired volume is the difference of the volume of the cone with a radius of B C = 1 3 6 0 and a height of A C = 1 3 1 4 4 , and the volume of the spherical cap ( V cap = 3 1 π h 2 ( 3 R − h ) ) where h = E C = 1 3 4 0 and R = O B = 5 .
Therefore, V = V cone − V cap = 3 1 π ( 1 3 6 0 ) 2 1 3 1 4 4 − 3 1 π ( 1 3 4 0 ) 2 ( 3 ⋅ 5 − 1 3 4 0 ) = 3 9 1 6 0 0 π , which means a = 1 6 0 0 , b = 3 9 , and a + b = 1 6 3 9 .