Geometry Proving Problem
True or false :
In a triangle A B C , ∠ A = 2 ∠ B . Let a , b and c denote the lengths of the sides of B C , C A and A B respectively. Then the equation a 2 = b ( b + c ) must be fulfilled.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Note: The question is equivalent to "Prove that B C 2 = A C ( A C + A B ) ".
We start by introducing a straight line A D with point D on line B C such that ∠ D A E = ∠ D B A = θ . Now, observe that ∠ C A D = θ , ∠ A D C = 2 θ , ∠ A C D = 1 8 0 − 3 θ . Therefore, we can also deduce that △ A C D ∼ △ E C A ( A A A )
Then, we can use this similarity to derive the following: B C A C = A C C D = A B A D ⇒ A D + C D A C = A C C D = A B A D ⇒ A D × C D + C D 2 = A C 2 and A D × C D + A D 2 = A B × A C
Then, substituting in, we get B C 2 = ( A D + C D ) 2 = A D 2 + C D 2 + 2 A D × C D = A C 2 + A C × A B = A C ( A C + A B )

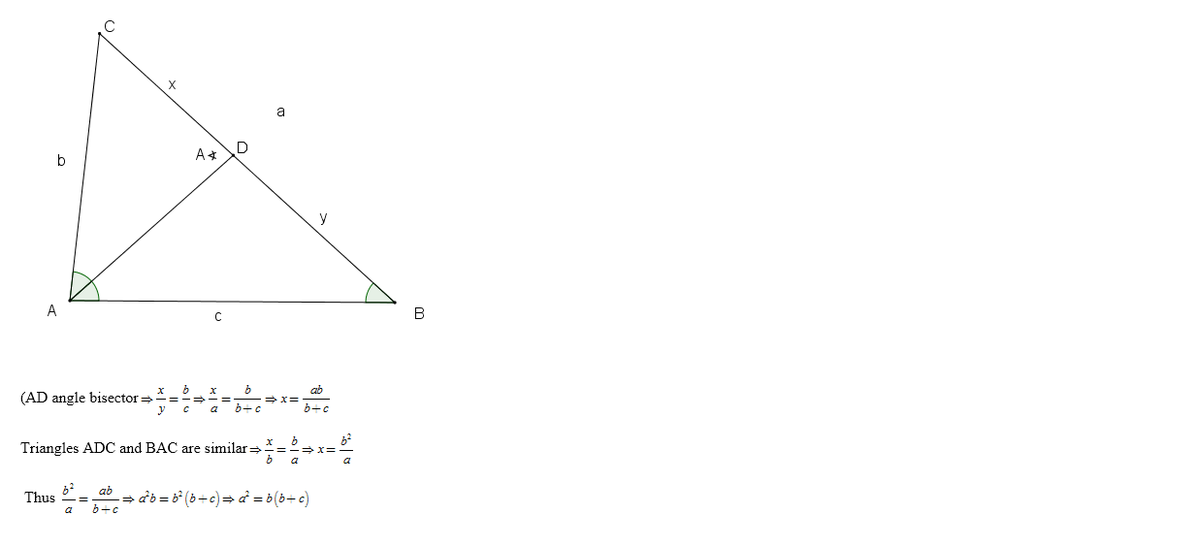
A = 2 B , C = π − 3 B ⟹ sin A = sin 2 B and sin C = sin 3 B = 3 sin B − 4 sin 3 B
Using a = 2 R sin A , b = 2 R sin B . . . so that statement is: sin 2 A = sin B ( sin B + sin C ) OR sin 2 2 B = sin B ( sin B + 3 sin B − 4 sin 3 B ) L H S : sin 2 B ( 4 − 4 sin 2 B ) = 4 sin 2 B cos 2 B = sin 2 2 B = R H S
Hence statement is True .