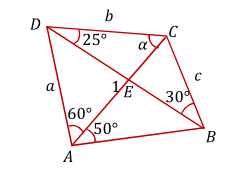
Geometry Question by Mithil Shah # 4

Const: Draw $\angle DBF = 60^{\circ}$ and produce the diagonal $AC$ to intersect $BF$ at $F.$ Join $DF.$

Let $\angle ADB = x^{\circ}$ Then $\angle ABD = 180^{\circ} - 110^{\circ} - x^{\circ} = (70-x)^{\circ}$ Clearly, Quadrilateral $ABFD$ is a $cyclic$ quadrilateral . => $\angle BAD = \angle BDF = 50 degrees => \angle CDF = 25^{\circ}$ , $\angle ADB = \angle AFB = x^{\circ}$ and $\angle ABD = \angle AFD = (70-x)^{\circ}$ .

Now have a look at the configurations in the $above$ diagram, $BC$ and $DC$ are the angle bisectors of $\angle DBF , \angle BDF$ respectively in $\Delta FBD$ . => C is the incenter. => $FC$ is the angle bisector of $\angle DFB$ . = $x^{\circ} = (70-x)^{\circ}$ => $x^{\circ}$ = $35^{\circ}$ . Now $\angle AEB = \angle AFB + \angle DBF$ = $x^{\circ}+60^{\circ} = 35^{\circ} + 60^{\circ}$ = $95^{\circ}$

$K.I.P.K.I.G.$

Circumscribe a circle about triangle DCB. Since m<CAB = 2 m<CDB and m<CAD = 2 m<CBD, we know A is the center of this circle. Extend CA to intersect the circle at C', which is the diametrically opposite point to C. Thus, C'B is a 130 degree arc, and CD is a 60 degree arc, so the pink angle must be (130+60)/2= 95 degrees

As is often the case, the solution is much easier to guess than to calculate. Below is the calculation.

We can arbitrarily set $AC=1$ and $AD=a$ . From $\triangle ACD$ using the law of cosines $DC=b=\sqrt{a^2-a+1}$

In the same triangle with law of sines $\alpha=arcsin(\frac{a}{b}sin(60^\circ))=arcsin(\frac{a\sqrt{3}}{2\sqrt{a^2-a+1}})$

From $\triangle BCD$ we know that $\angle BCD=125^\circ$ so $\angle BCA=125^\circ-\alpha$ and in $\triangle ABC$ the $\angle ABC=180^\circ-50^\circ-(125^\circ-\alpha)=5^\circ+\alpha$ .

From law of sines in $\triangle ABC$ we get $sin(5^\circ+\alpha)=\frac{sin(50^\circ)}{c}$

But $c$ from $\triangle BCD$ is $\frac{c}{sin(25^\circ)}=\frac{b}{sin(30^\circ)}$

Putting it together into a single equation for $a$ we get

$sin(5^\circ+arcsin(\frac{a\sqrt{3}}{2\sqrt{a^2-a+1}}))=\frac{sin(50^\circ)}{sin(25^\circ)}\frac{sin(30^\circ)}{\sqrt{a^2-a+1}}$

The solution of this equation is $a=1$ , so the $\triangle ACD$ is equilateral and $\alpha=60^\circ$

From $\triangle CDE$ the $\angle CED=180^\circ-60^\circ-25^\circ=95^\circ$ , which means $\angle AEB=95^\circ$ .