Geometry Question on a equilateral triangle (Triangle and Square)
ABCD is a square, and △DPC an isosceles triangle with base angles of 15 degrees (∠PCD = ∠PDC = 15°).
Prove that △PAB is an
equilateral
triangle.
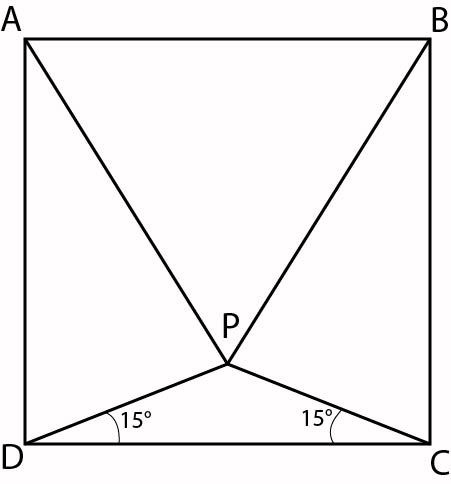 The drawing
The drawing
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
What do you mean by that?
Let P ′ be a point such that A B P ′ is equilateral. e.g ( A B = A P ′ = B P ′ )
Then we get that ∠ P ′ A D = ∠ P ′ B C = 3 0 ∘
Since A D = A P ′ = B P ′ = B C , we get that ∠ A P ′ D = ∠ B P ′ C = 7 5 ∘
We then get ∠ D P ′ C = 1 5 0 ∘ and Δ P ′ D C ≅ Δ P D C and since P and P ′ lie inside the square. We get P ≡ P ′ .
Note that we made use of the phantom point P ′ to arrive to our conclusion.
If you assume the side of the square to be 2, then the distance between P and CD is t a n ( 1 5 ∘ ) = 2 − 3 .
The distance of P from AB, if ABP is an equilateral triangle with side 2 is 3 .
The vertical distance between AB and CD, measured at P, is therefore 2 − 3 + 3 = 2 as required.
∠ C A B = ∠ C B A = 1 5 . Draw Δ B E D congruent to Δ A B C , so that ∠ E B D = ∠ E B D = 1 5 . Then since ∠ C B E = 6 0 and C B = E B , Δ C B E is equilateral triangle. Therefore C E = B E and Δ C E D and Δ B E D are congruent. Hence C D = D B = F D , so that Δ C D F is equilateral triangle with all angles 6 0 .