Geometry + Radical Arithmetic = Headache!
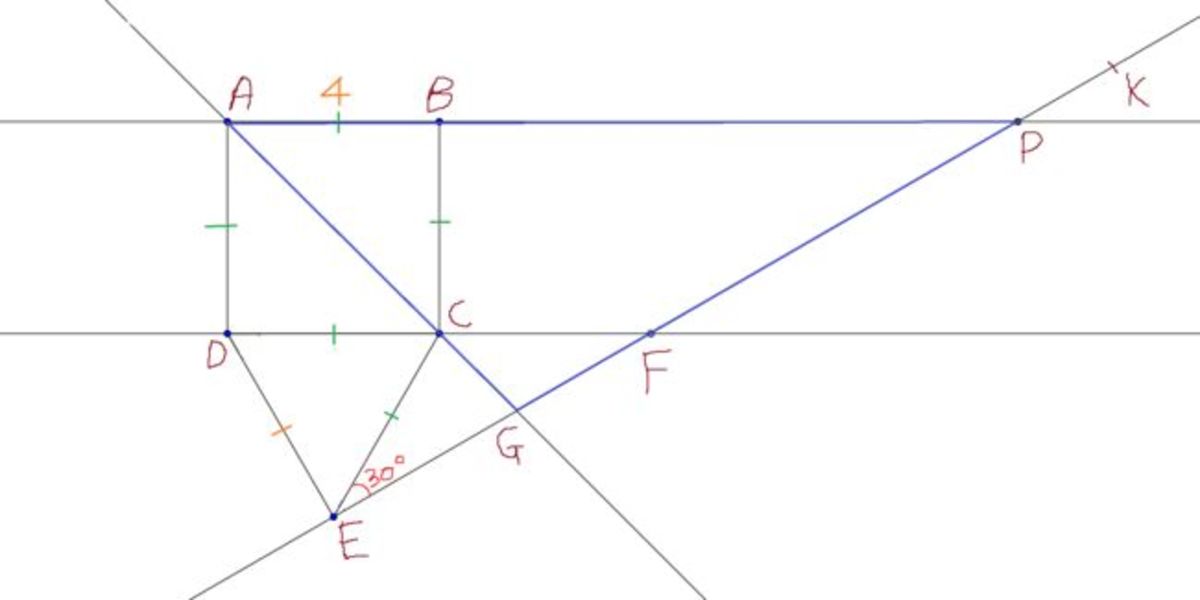
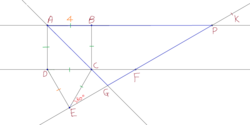 Consider a square
A
B
C
D
with side of length
4
.
Consider a square
A
B
C
D
with side of length
4
.
Let E be a point outside A B C D such that Δ C D E is equilateral.
Draw ∠ C E K = 3 0 ∘ such that ray E K intersects ray A C at G , ray D C at F , ray A B at P .
If Area of Δ A G P can be represented as:
a + b c where c is independent of a perfect square.
Find a + b + c .
The answer is 35.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Almost the same 'method' as yours , only the difference is I dropped just 1 perpendicular and I did not use trigonometry.BTW nice solution.
So we know that C E = 4 a n d ∠ C G E = 7 5 ∘
So applying Sine law in Δ C G E
S i n 3 0 C G = s i n 7 5 ∘ 4
We get C G = 3 + 1 4 2 .
Hence A G = A C + C G = 4 2 + 3 + 1 4 2
= 3 + 1 4 2 ( 3 + 2 )
Now ∠ A P G = 3 0 ∘ applying sine law in Δ A P G
S i n 3 0 A G = s i n 4 5 ∘ P G
We get P G = 3 + 1 8 ( 3 + 2 )
Now a r ( Δ A P G ) = 2 1 × A G × P G × s i n ∠ A G P
Substituting values we get a r ( Δ A P G ) = 2 0 + 1 2 3
Hence 20+12+3=35
I did it by dropping G H ⊥ A P . Then using extension of Pythagoras theorem , 4 5 − 4 5 − 9 0 and 3 0 − 6 0 − 9 0 triangles , I went on computing the sides one by one.At last I used 2 1 × b × h for area. :)
Log in to reply
Was it lengthier or smaller? and in problem you should add that c is a prime no. and something like that .i wasted one chance in that as i forgot to simplify it.
Absolutely the same way I did it
We know that C E = 4 a n d ∠ C G E = 7 5 ∘ So applying Sine law in Δ C G E 4 C G = s i n 7 5 ∘ s i n 3 0 o . s i n 7 5 o = 4 6 + 2 . ∴ C G = 3 + 1 4 2 = 2 2 ( 3 − 1 ) . ∴ A G = A C + C G = 4 2 + 2 2 ( 3 − 1 ) = 2 2 ( 3 + 1 ) . ∴ C G A G = 2 2 ( 3 − 1 ) 2 2 ( 3 + 1 ) = ( 3 + 2 ) . ∴ ( C G A G ) 2 = 7 + 4 3 . . . . . . ( 1 ) A r e a Δ G C F = 2 1 ∗ C F ∗ C G ∗ s i n ∠ F C G = 2 1 ∗ 4 ∗ 2 2 ( 3 − 1 ) ∗ 2 1 = 4 ∗ ( 3 − 1 ) . . . . ( 2 ) A r e a Δ A G P = ( C G A G ) 2 ∗ A r e a Δ G C F = ( 1 ) ∗ ( 2 ) = ( 7 + 4 3 ) ∗ 4 ∗ ( 3 − 1 ) = 2 0 + 1 2 3 . 3 5
same solution as yours
I think I was using the method of Nihar Mahajan . It is as follows:
Let the perpendiculars from E and G to A P be E H and G I and their lengths be h 1 and h respectively, and A P = b .
We note that ∠ A P E = 3 0 ∘ , therefore,
E H P H = h 1 b − 2 = cot 3 0 ∘ = 3
⇒ h 1 b − 2 = 4 + 4 sin 6 0 ∘ b − 2 = 4 + 2 3 b − 2 = 3 ⇒ b = 8 + 4 3
We also note that ∠ P A G = 4 5 ∘ , therefore, A I = G I = h , then we have:
G I P I = G I A P − A I = h b − h = cot 3 0 ∘ = 3 ⇒ b − h = 3 h
⇒ h = 1 + 4 3 8 + 4 3 = 2 ( 8 + 4 3 ) ( 3 − 1 ) = 2 + 2 3
The area of △ A G P ,
A = 2 1 b h = 2 ( 8 + 4 3 ) ( 2 + 2 3 ) = 2 0 + 1 2 3
⇒ a + b + c = 2 0 + 1 2 + 3 = 3 5