It's staring at me
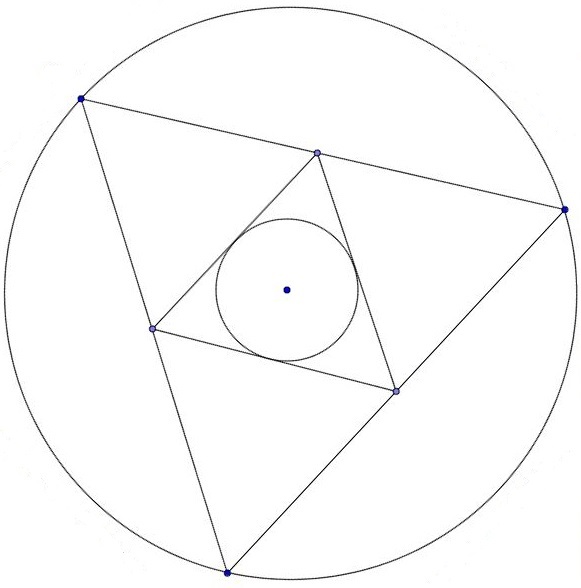 Let
Δ
A
B
C
be a triangle with vertices
A
=
(
0
,
0
)
,
B
=
(
6
,
0
)
,
C
=
(
3
,
3
3
)
,
and
Δ
P
Q
R
the pedal triangle of
Δ
A
B
C
.
Let
Δ
A
B
C
be a triangle with vertices
A
=
(
0
,
0
)
,
B
=
(
6
,
0
)
,
C
=
(
3
,
3
3
)
,
and
Δ
P
Q
R
the pedal triangle of
Δ
A
B
C
.
The sum of the circumradius of Δ A B C and inradius of Δ P Q R can be expressed as c a b for positive integers a , b , and c , where a , c are coprime and b is square-free.
Find a × b × c .
The answer is 30.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
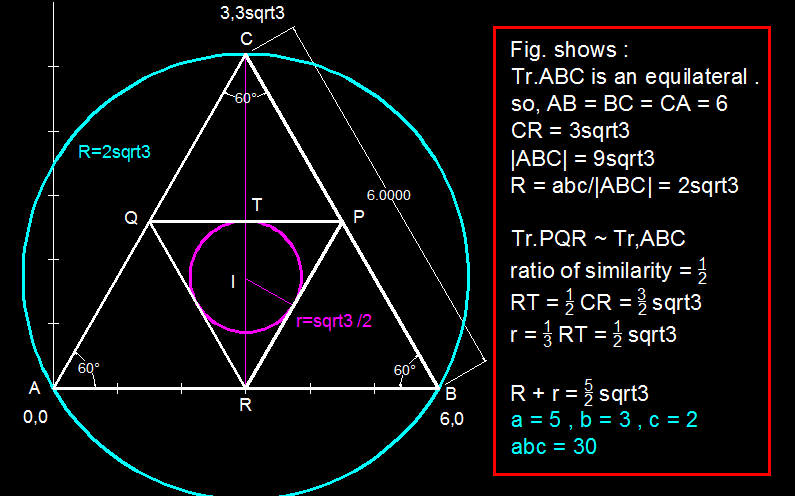
Since the midpoint M of AB is also (3,0), CM is the altitude of isosceles triangle CA=CB.
Slope of AC =
3
, so angle CAB=60.
So ABC is equilateral side 6. R=
2
3
.
Hence pedal triangle also equilateral side 3.
Pedal inradius 1/2 its Circumradius=1/2 * 1/2 * R.
Required sum
2
3
(
1
+
4
1
)
=
2
5
∗
3
a * b * c=5 * 2 * 3=30.