Geometry with a Square
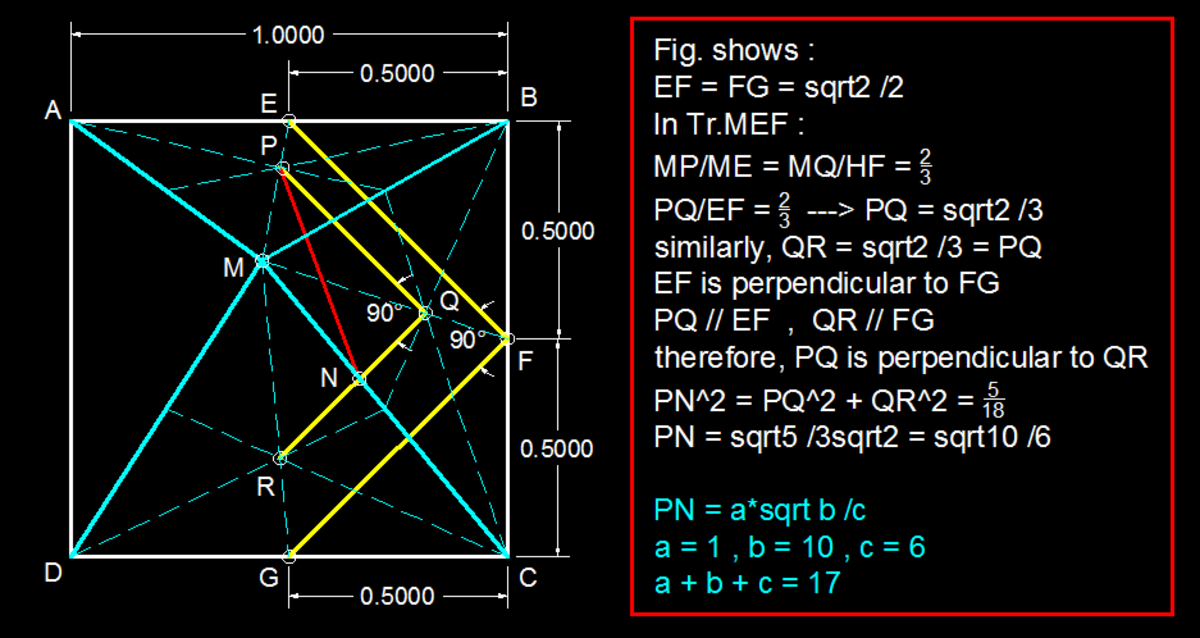
Let M be an arbitrary point inside a unit square A B C D . Consider points P , Q , R defined as points of intersection of medians of △ A B M , △ B C M , △ C D M . The length of the segment between P and midpoint of Q R can be expressed as c a b , find a + b + c .
The answer is 17.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
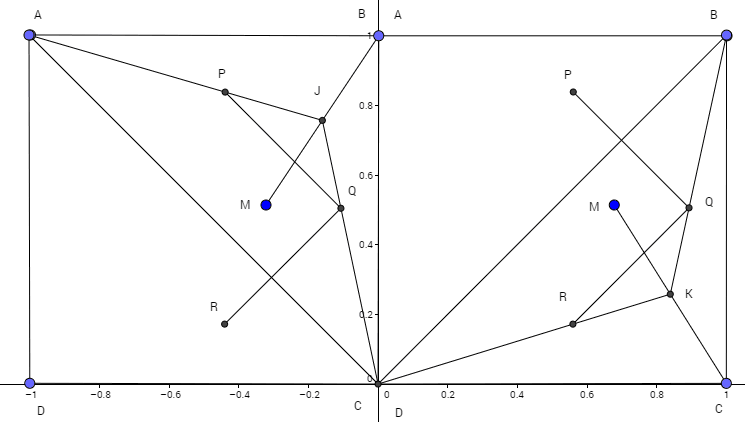
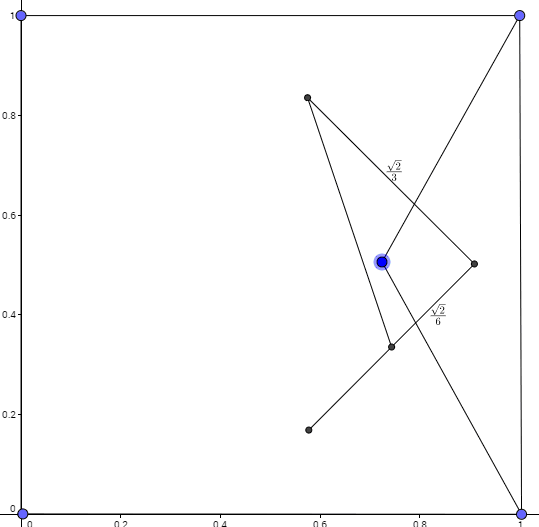
Images from https://app.geogebra.org/#geometry
Since P,Q and R are the intersections of medians, they are the centroids of △ A B M , △ B C M and △ C D M .
For clearer illustration, I have drawn 2 squares, square X on the left and square Y on the right.
A property of centroids is that the distance from a vertex to the centroid is 3 2 the length of the median.
Let J be the midpoint of MB and K be the midpoint of MC.
In square X, △ P J Q ∼ △ A J C so P Q ∥ A C and P Q = 3 1 A C = 3 2
Similarly, in square Y, △ Q K R ∼ △ B K D so Q R ∥ B D and Q R = 3 1 B D = 3 2
Also, AC and BD are perpendicular. Since P Q ∥ A C and Q R ∥ B D , we see that ∠ P Q R = 9 0 ∘ .
Direct application of Pythagorean Theorem gives D i s t a n c e = ( 6 2 ) 2 + ( 3 2 ) 2 = 6 1 ∗ 1 0
⇒ a + b + c = 1 + 1 0 + 6 = 1 7