Germanian Geometranian!
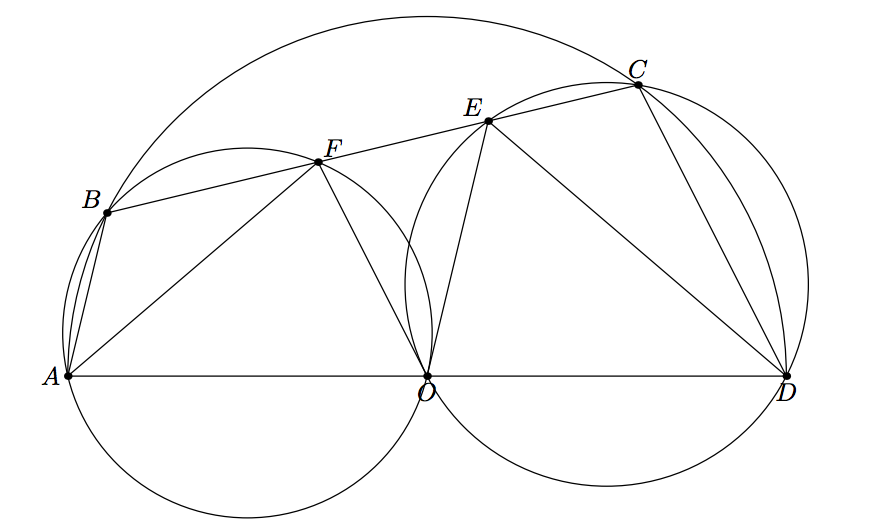
Let points and lie on the circle with diameter and center on the same side of . The circumcircles of triangles and meet at points and respectively.
Find the radius of the given circle if and .
The answer is 8.944.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
First we can draw all the diagonals to the cyclic cuadrilaterals: O C , O B , B D and A C . Let ∠ A D E = α , therefore we can use circle properties, from which:
∠ O D B = ∠ O C B = ∠ O B C = ∠ O A F = α
And
∠ O A C = ∠ D B C = ∠ O C A = β ⇒ ∠ D O C = ∠ D E C = 2 β ⇒ ∠ B D E = β
Therefore:
B F = E D = 1 0 ⇒ △ A O C ∼ △ B E D
And
∠ C A F = ∠ A C F = ∠ O B D = ∠ O D B = α − β ⇒ △ O D B ∼ △ F A C
As those triangles are proportional to each other, we have:
A C r = B D 8 ∧ B D r = A C 1 0 ⇒ r = 8 0