Get back to business...IIl

Geometry Level 2

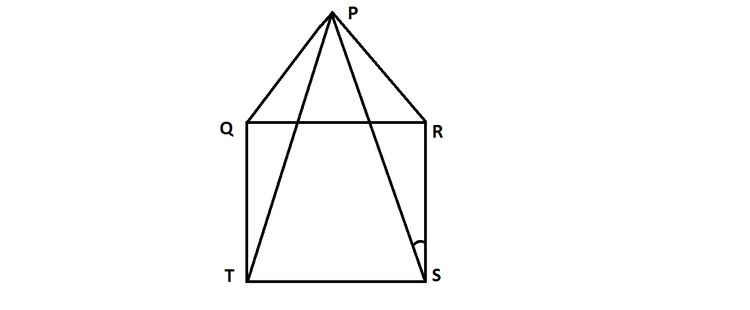In the given fig., POR is an equilateral Triangle & QRST is a Square. Find angle PSR....

3 solutions

Archiet Dev
Jun 13, 2014

Each Side of a square has an angle of 90 degree...&

Each Side of an equilateral Triangle has an angle 60 degree....

So, angle PRS =90+60 = 150 degrees

Now on Triangle PRS

An.RPS = An. RSP {Isosceles Triangle Property or PR = RS(Because RS = QR = PR) }

So,According to Angle sum property of Traingles

Let an.RPS = x =An. RSP

=> x + x + 150 = 180

=> 2x = 180 - 150

=> x = 30 / 2

=> x = 15 degrees

So,an PSR is equals to 15 degree...

Okk ,,,,,,,,,,

Anubhav Sinha - 6 years, 10 months ago

I Don't understand why did you add the 90 and 60 angles and put it as PRS... Explain T_T

Moheb Mohi - 6 years, 10 months ago

Because an. QRS is vertex angle of square and an. QRP is vertex angle of equilateral triangle.
Hence, 90 + 60 = 150 degrees

Archiet Dev - 6 years, 2 months ago

Mehul Arora
Oct 25, 2014

An. PRQ = 60 Degrees.(All angles of an equilateral triangle is 60 degrees)

Angle QRS = 90 Degrees (All angles of a square is 90 degrees)

QR is a common side Hence sides of the traiangle and square are equal.

Therefore Triangle PRS is an isoceles triangle with angle PRS equal to 150 Degees.

Hence An. P= An. S = x (say)

Therefore !50 Degrees + 2x= 180 Degrees.

Answer = Therefore An.S= X= 15 Degrees

Raghavendra Srinivas
Jul 17, 2014

PQ=QT from question equal sides of square and triangle,angle TQP is 150 and Triangle PQT is isosceles hence 15 degrees