Get back to business...V
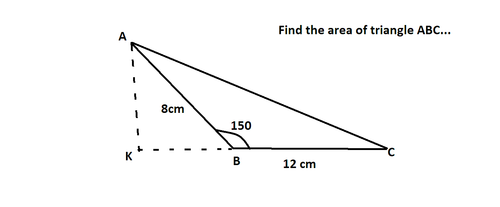 In Triangle
ABC ,AB= 8 cm ,BC= 12 cm
*An.
ABC=150
.
Then,Find the Area of *Triangle
ABC
...
In Triangle
ABC ,AB= 8 cm ,BC= 12 cm
*An.
ABC=150
.
Then,Find the Area of *Triangle
ABC
...
The answer is 24.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
7 solutions
Give Angle ABC = 150, its supplement, Angle ABK, must be 30. That makes Triangle ABK a 30:60:90 and thus side AK must be half the hypotenuse because it is opposite the 30 degree angle and all 30: 60: 90 triangles have sides in proportion a : a(sqrt { 3 }): 2a. As side AK is also the height of Triangle ABC, we have Area = 1/2 4 12 = 24.
@Michael Goldenberg Sir do you know the formula .5a b sin theta?That is an easier way of solving this.
Area of a triangle = 0.5 a b*sin x where x is the included angle between the sides a and b.
Easy problem
Why can't i use the cos rule Assuming that area=AB 2 +BC 2+ 2 ABxBC Cos 150 ???
Moheb Mohi, that formula gives you the squared length of the side AC, not the area.
actually the question should not have included the construction of perpendicular, it would be more elementary
@akash i agree
I'll keep that in mind...Thanks
Log in to reply
Why can't i use the cos rule Assuming that area=AB 2 +BC 2+ 2 ABxBC Cos 150 ???
1/2 X 8 X 12 X sin 150 = 4 x 12 x 1/2 = 24
The angle ∡ A B C = 1 5 0 ° , we can assume that A K is an altitude of the triangule A B C . So ∡ A B K = 3 0 ° and ∡ B A K = 6 0 ° ; so the triangle A K B is half of an equilateral triangle, so 2 A K = A B so A K = 4 . So the area is 2 4
If the angle is 150º, your complement is 30º. Thus, sin 30º= 1/2. Then AK is x, sin 30º = x/8, 1/2 = x/8 --> 2x = 8 --> x = 4
If AK = 4, hence, the area of triangle ABC is height versus base divided by 2. AK is height and BC is base, then area of triangle is: (4 x 12) / 2 --> 48/2 = 24. The answer is 24 cm².
@Heder Oliveira Dias One the first lin you said the complement of 130 is 30 change 130 to 150
Ok... thanks...
direct application of A r e a = 2 1 a b s i n θ
2 1 8 × 1 2 × s i n 1 5 0 = 2 4