Get Started With Combinatorics 1 – Alice, Bob, and Charlie
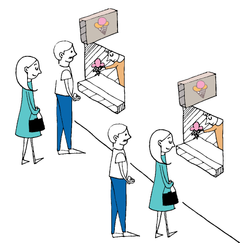 If Alice and Bob want to stand in a line, there are two possible orders in which they can stand (see above).
If Alice and Bob want to stand in a line, there are two possible orders in which they can stand (see above).
However, Charlie is in their group today, so there are more possibilities. How many orderings exist for three people standing in line?
The answer is 6.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
12 solutions
Or you could simply do 3 ! = 3 × 2 × 1 because there are 3 ways for the first person, 2 for the next, and 1 for the last.
Log in to reply
Alex, my sincere thanks to you for your explanation of factorials in this context. I've always known the factorial since my classroom days of probability, but I don't think I've ever EVER run across as simple an explanation of how it really works until you just stated it above.
Sadly, I feel smarter and dumber at the same time! =]
For the people who are asking for clarification, the "!" is a mathematical symbol. It refers to a factorial, which is taking the number prior to it and multiplying it by every positive integer lower than it.
4! = 4 3 2 1 = 12 2 1 = 24 1 = 24
In this problem, we use 3! because for the first position, there are 3 possibilities. Once the first position has a person dedicated to it, that person cannot be in two places at once, so there are now only two people to fill the second place in line. So on and so forth.
For a deck of cards, there are 52! orders possible for the entire deck. That's 8.066*10^67 possible orders!
If I take 3 minutes to break a rop in 2 pieces, then how many minutes will be required to break it in 3 pieces
Log in to reply
6 minutes 2 piece means 1 cut then 3 pieces means 2 cut.
What if there were 2 lines? How many permutations would there be? would be simply be 3! times 2?
Log in to reply
Well if there are 3 different people in each line and those people did not switch lines then yes it would 3! x 2
It would be easy for the beginners to understand the formula better,if this type of explanation is given.But it would be better if the formula is also given.Can we write out all the combinations if we were dealig with a que of 1000 people? THe whole idea behind Combinatorial Maths is speedier solution to such problems.
We are dealing with a 'permutation without repetition'
A 'permutation' is a combination wherein the ordering of objects matters.
For example, the ordering ' C h a r l i e , A l i c e , B o b ' is different from ' A l i c e , C h a r l i e , B o b '
We say 'without repetition' since no one can be both first and second in line at the same time.
For example, the ordering ' C h a r l i e , C h a r l i e , C h a r l i e ' is invalid since this would mean that Charlie has 2 clones standing in line with him.
The formula for permutations without repetitions is ( n − r ) ! n ! wherein n is the number of objects
r is the number of objects that you need and n ! = n ∗ ( n − 1 ) ∗ ( n − 2 ) ∗ ( n − 3 ) ∗ . . . ∗ 3 ∗ 2 ∗ 1 For example, 5 ! = 5 ∗ 4 ∗ 3 ∗ 2 ∗ 1 (Note: 0 ! = 1 )
In this case n = r = 3 since we have three objects: Alice, Charlie and Bob, and we are going to need all of the three of them because we are going to put all of them in a line
Substituting this in the formula mentioned earlier, we have ( 3 − 3 ) ! 3 ! → 0 ! 3 ∗ 2 ∗ 1 → 1 6 → 6
if we cross product any set of 3 numbers with itself the no. of elements new set contain 3x3= 9 elements out of which 3ordered pair contain same elements so they are eliminated and remaning one element was added in each ordered pair and thus we get 6 orders for eg -A{123} so AXA={(123)(123)}={(1,1),(1,2),(1,3),(2,1),(2,2),(2,3),(3,1),(32),(3,3)} ordered pair containing smae element=(1,1),(2,2),(3,3) these are eliminated remaining are=(1,2),(1,3),(2,1),(2,3),(3,1),(3,2) remaining elements in each ordered pair makes different orders=(1,2,3) (1,3,2),(2,1,3),(2,3,1),(3,1,2),(3,2,1) so there are six possible orders and thus answer is =6
For the person in front you can choose any one of them (3). For the person behind them you'll only have two choices, and that'll leave you with no choice for the one at the back. So it's 3 times 2 (times 1), or 3!.
The different orders are six in no. i. e: 1 Alice, Bob, Charlie.
2 Charlie, Bob, Alice.
3 Bob, Charlie, Alice.
4 Charlie, Alice, Bob.
5 Bob, Alice, Charlie.
6 Alice, Charlie, Bob.
What I do for these problems is square the number of choices(3 in this case), and subtract the number of choices from the result to remove the identicle pairs, if that makes sense. 3*3=9 9-3=6
3! Factorial way is proper to get the exact solution
3 people in row. so,the of ways, 3!=3 2 1=6
Answer :- 6
It's a permutation without repetitions. So The answer is 3!=6
Let's list the 3 people in line:
Alice A, Bob B, Charlie C
- ABC
- CAB
- BCA
- ACB
- BAC
- BCA
And that's 6 possible orders for those 3 to stand in line
2 people in line 2x1...3 in line 3x2x1
There it are 3 posibilities, then it are 2 posibilities and finally it are1 posibility. Hence 3+2+1=6
Moderator note:
Shayla is right, if you had 10 people instead of 3, you would have a total of 1 × 2 × 3 × … × 1 0 ways, and not 1 + 2 + 3 + … + 1 0 ways.
3×2×1, not 3+2+1
Let's list out the number of ways:
Hence, there are 6 orderings for three people to stand in line.