Getting back to the old things #2
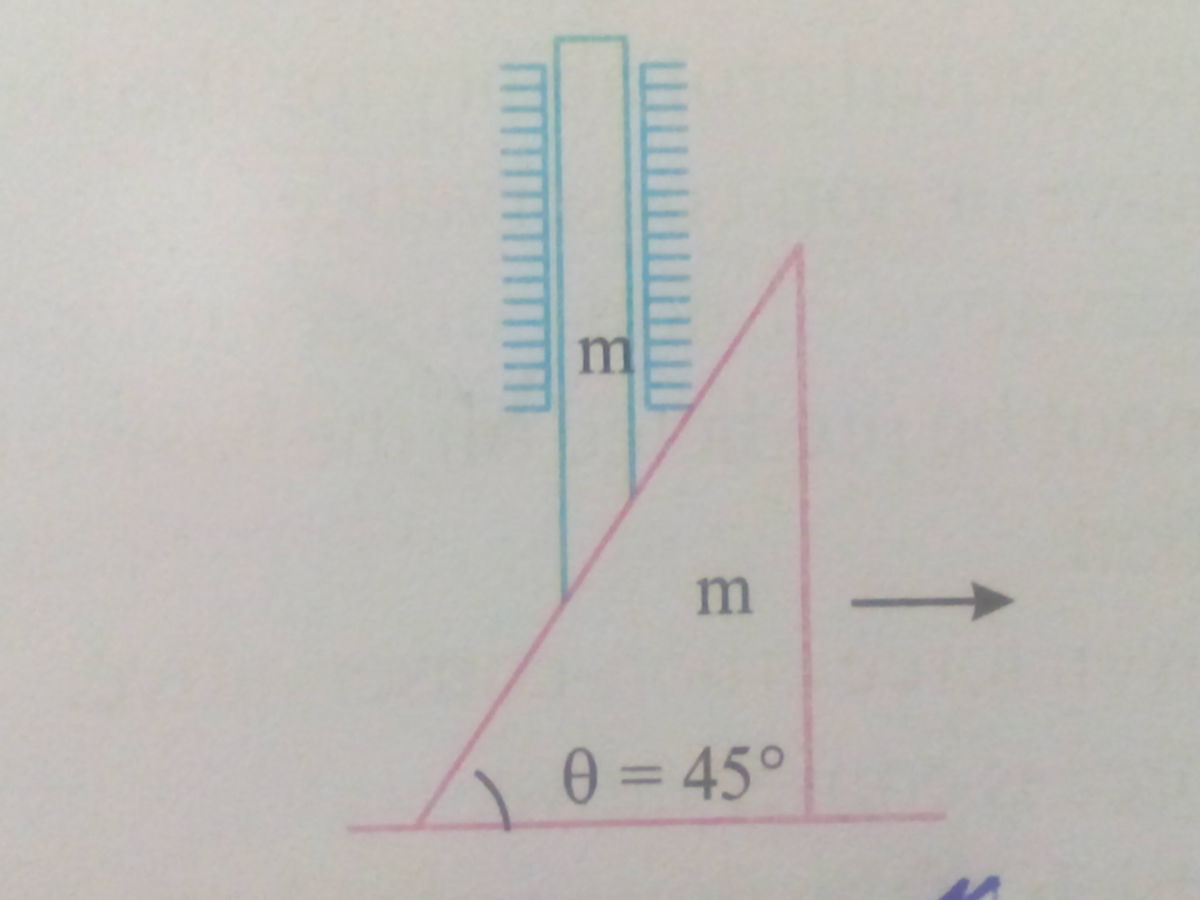 A smooth vertical rod is released from rest such that it is constrained to move along a smooth wedge as shown. The angle of the incline is
. When the wedge moves through a distance
, the speed of the rod will be
. Find the value of
up to 3 decimal places.
A smooth vertical rod is released from rest such that it is constrained to move along a smooth wedge as shown. The angle of the incline is
. When the wedge moves through a distance
, the speed of the rod will be
. Find the value of
up to 3 decimal places.
The answer is 1.000.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Apart from horizontal reaction forces keeping the rod in place, the only forces acting on the rod are gravity and the normal reaction force N from the wedge. Equally, the only force acting on the wedge that has a horizontal component is the normal reaction N from the rod.
Since the angle of incline of the wedge is 4 5 ∘ , the distance fallen by the rod and the horizontal distance moved by the wedge are always the same, and so the downwards acceleration of the rod is equal to the horizontal acceleration a of the wedge. Thus we have the equations m a = m g − 2 1 N m a = 2 1 N which together imply that a = 2 1 g . Thus, when the wedge has moved a distance x , is has speed 2 a x = g x , which means that a = 1 .