Getting Robo to Safety
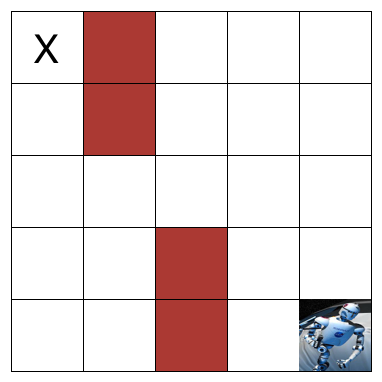 Betty wants to create an algorithm to help the NASA robot get from the lower right corner to the top-left square marked with a X. However, it cannot step on the red tiles, as they represent a lava river.
Betty wants to create an algorithm to help the NASA robot get from the lower right corner to the top-left square marked with a X. However, it cannot step on the red tiles, as they represent a lava river.
Which of these algorithms could she use?
Algorithm 1: Walk 4 squares up and 4 squares left.
Algorithm 2: Walk 2 squares up and 4 squares left and 2 squares up.
Algorithm 3: Walk 2 squares left and 4 squares up and 2 squares left.
Algorithm 4: Walk 4 squares left and 4 squares up.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Deserves an upvote.+1
Log in to reply
Thanks! :)
I'll try adding a graphical explanation too later.
You said:
Walk 3 squares northwest (diagonally).
Walk 1 square left.
Walk 1 square northwest again (diagonally).
Walk 1 square up (reaching X).
By walking 3 squares northwest (diagonally), won't the robot burn in lava? You mean 2 squares northwest?
Log in to reply
Ah sorry, I meant 2 squares, not 3. Let me edit it! Thanks for pointing out the mistake. :)
Technically, if we consider the robot as a point mass starting from the upper left corner of the bottom right box, the shortest distance it has to travel to reach the upper left box is 1 + 2 + 5 squares.
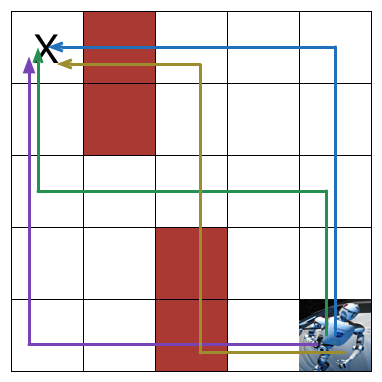
Algorithm 1 - Blue line
Algorithm 2 - Green line
Algorithm 3 - Yellow line
Algorithm 4 - Purple line
Clearly only algorithm 2 would work.
Little known fact: If they accidentally drive into a lava river they can use ↑ ↑ ↓ ↓ ← → ← → B A and they'll get 99 extra lives .
just think and solved the question
We need to follow an algorithm which avoids stepping onto any of the red tiles throughout the entire duration of the execution of the algorithm.
Note: Here, while explaining Algorithm 2 , we considered that the robot doesn't vaporize when it first steps on a red tile and hence we show that that algorithm has the potential to damage the robot 3 times. In reality, Algorithm 2 causes the robot to vaporize just as it steps on the first red tile it encounters, i.e., halts on the second step.
From the analysis, it's obvious that Algorithm 2 is the only algorithm among the given four that avoids stepping into any of the red tiles and is hence, the algorithm Betty could use.
A follow-up question would be to find the shortest algorithm possible if diagonal movements are allowed too. In that case, we use the fact that the straight line distance between two points is the shortest distance and get the shortest algorithm as follows:
This algorithm is of 5 steps and can easily be observed to be the shortest possible algorithm if we allow diagonal movements. If we only allow horizontal and vertical movements, it's quite obvious that Algorithm 2 is the shortest possible algorithm in that case.