Getting to 1653
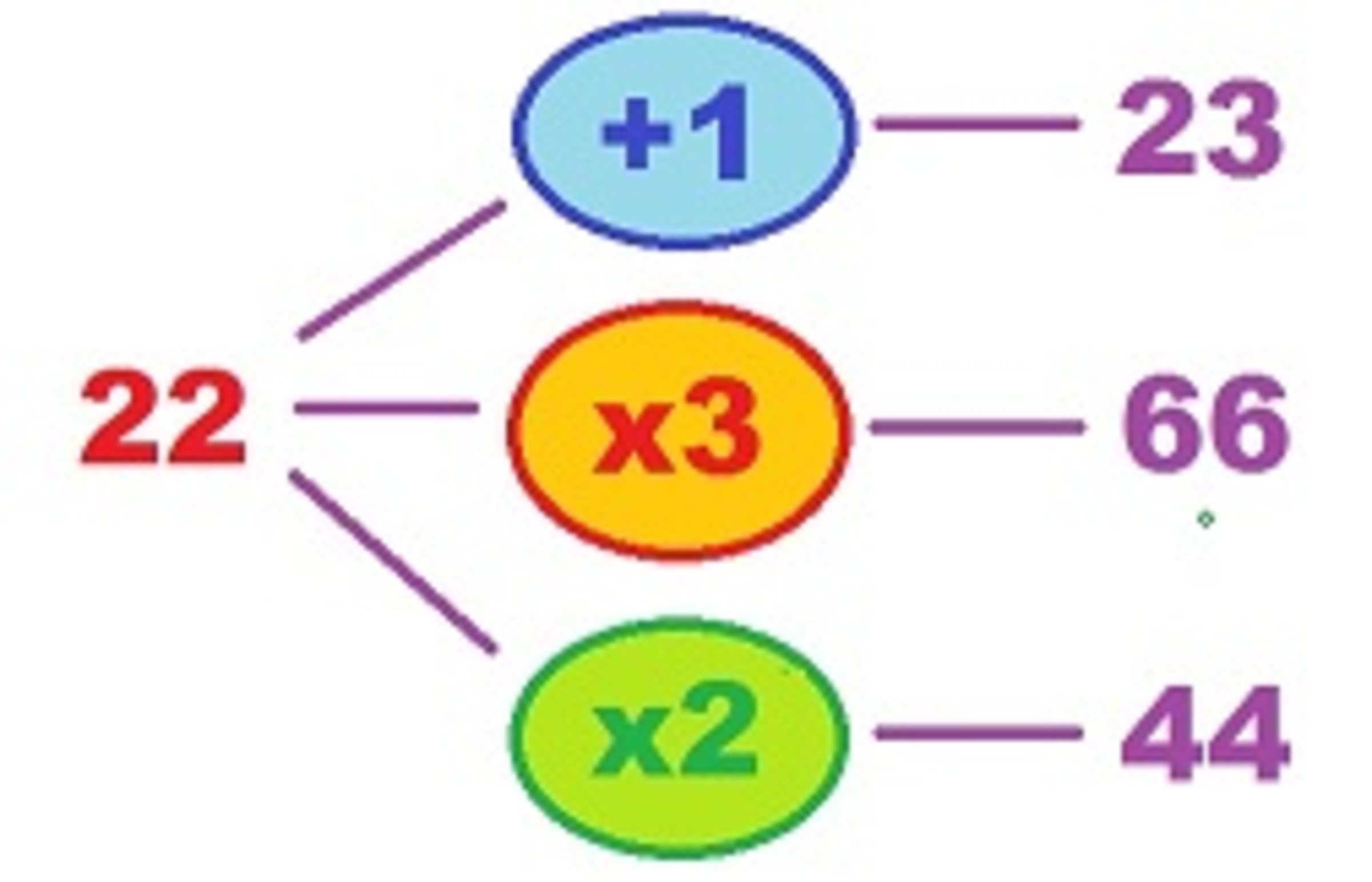
You start with .
Then, as many times as you like, you can choose to perform one the following operations: , , or
What is the fewest number of operations you would need to perform to get to ?
For example, you could get to with the following operations:
And, that would be considered operations.
The answer is 12.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The minimum number of operations can be solved by the following recursion relation:
Where f i ( n ) = i n if n divides by i , ∞ otherwise
This is because there are at most three ways to get to n :
Solving, A ( 1 6 5 3 ) = 1 2
One such minimal set of operations to give you 1 6 5 3 is the following:
+ 1 → × 3 → × 3 → + 1 → × 2 → × 3 → + 1 → × 3 → × 3 → + 1 → + 1 → × 3
And I know that @Pi Han Goh is going to want me to find a simpler solution that doesn't involve recursion like this, and, yes, I'll think about that, but for now this is the best I got! :-P