Give and Take

Electricity and Magnetism Level 3

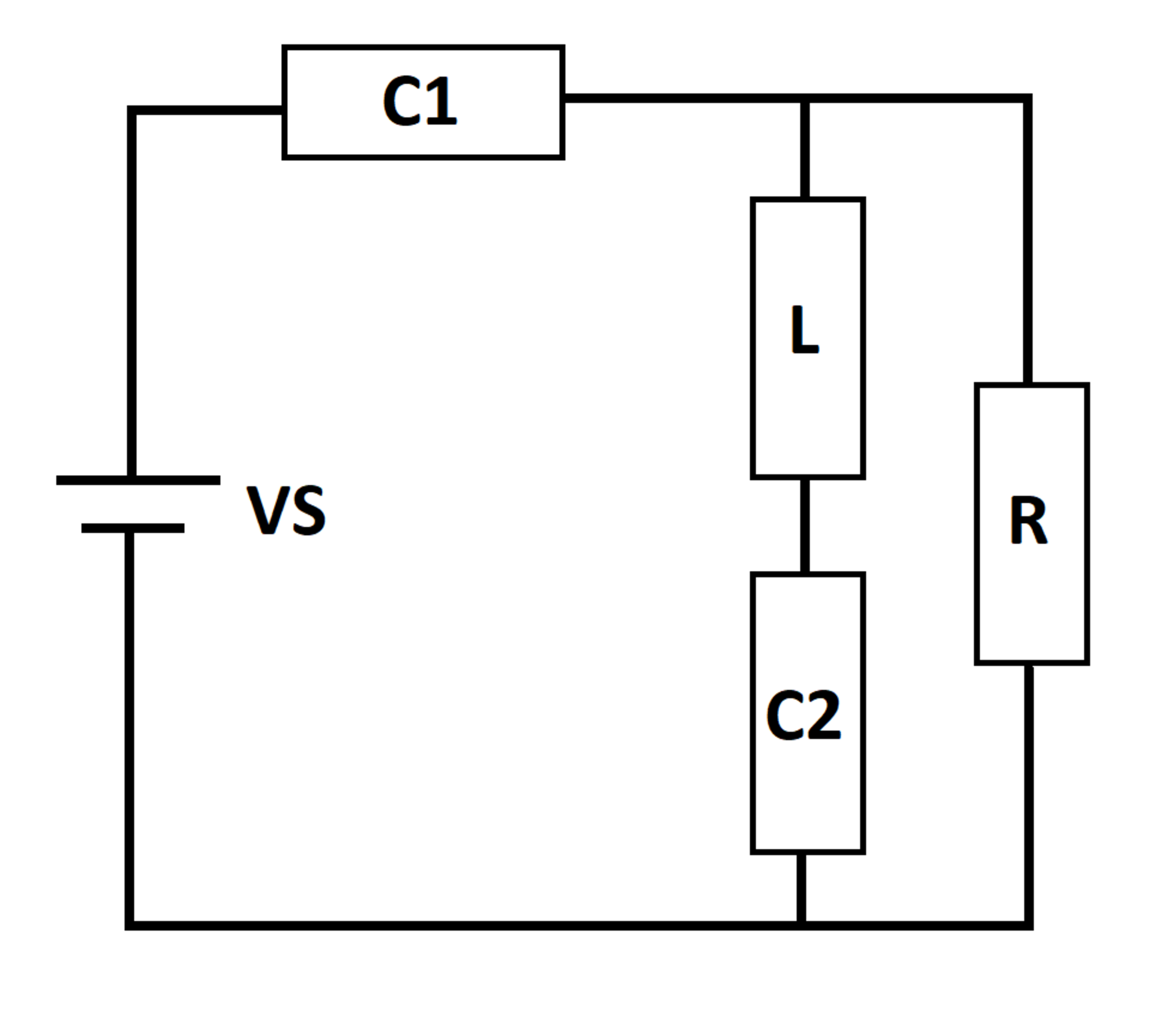
A DC voltage source excites an RLC circuit. At time $t = 0$ , the inductor and capacitors are de-energized. Let $E_S (t)$ be the cumulative energy supplied by the source to the rest of the circuit, as of time $t$ .

Let $E_{S \infty}$ be the value of $E_S (t)$ as $t$ approaches infinity. Let $E_{S max}$ be the largest value of $E_S (t)$ over all time.

What is $\Large{\frac{E_{S max}}{E_{S \infty}}}$ ?

Details and Assumptions:
1) $V_S = 10$
2) $R = 1$
3) $L = 1$
4) $C_1 = 1$
5) $C_2 = 1$

The answer is 1.105.

1 solution

Karan Chatrath
Jan 2, 2020

The solution method will be brief. I will focus more on the results.

Let the source current be $I$ , current through inductor be $I_2$ and that through the resistor be $I_1$ . The charge on capacitor $C_1$ is denoted as $Q$ and that on capacitor $C_2$ is $Q_2$ . Circuit equations are:

$V_S = L\dot{I}_2 + \frac{Q}{C_1} + \frac{Q_2}{C_2}$ $I_1R = L\dot{I}_2 + \frac{Q_2}{C_2}$ $I = I_1 + I_2 \ ; \ \dot{Q} = I \ ; \ \dot{Q_2} = I_2$

The initial conditions can be computed by recognising that each capacitor has no charge at $t=0$ , the current through the inductor is zero at that instant and the current through the resistor is $I(0)=10A$ . Numerical integration yields the answer of $\boxed{1.1046}$ . What is really interesting about this problem can be summarised in the plot below:

$E_S$ is the energy provided to the circuit by the source, $E_R$ is the energy lost as heat in the resistor, $E_L$ , $E_{C_1}$ and $E_{C_2}$ are the energies stored in the other electrical elements.
At steady state, half the energy provided to the circuit is lost as heat and half of it is stored in the capacitor $C_1$ .
No energy is stored in capacitor $C_2$ . This is a bit strange. So what is essentially happening is that the capacitor $C_2$ initially charges and then discharges losing all energy it gained. The same line of argument applies to the inductor. There is a buildup and then decay of current through the inductor. This behaviour can be seen in the yellow and green curves.
What this plot also illustrates is the applicability of the energy conservation principle. If the signals shown in red, purple, yellow and green were to be added up, one would obtain exactly the blue curve which is $E_S$ .

Those plots are very nice, thanks. I hadn't realized the one-half property. One property I observed is that $E_{S \infty}$ always ends up being the square of the source voltage (with these circuit parameters, at least)

Steven Chase - 1 year, 5 months ago

Interesting observation. If I think about it carefully, it does make sense too.

$E_S = \int_{0}^{\infty} \left(V_S I(t)\right) dt$

Andthe current expression can be arranged to resemble a structure of Ohm's law, and can be written without loss of generality as:

$I(t) = \frac{V_S}{R}f(R,C_1,C_2,L,t)$

The function $f$ would comprise of decaying exponentials (multiplied with sinusoids) which would be negligible after a significant amount of time, just leaving the steady-state term. From here, for this given set of parameters, this result should follow. Of course, a closed-form solution would be needed to confirm this line of thought.

Karan Chatrath - 1 year, 5 months ago

Give and Take

The answer is 1.105.

1 solution

0 pending reports