Frictionless Slide Propulsion
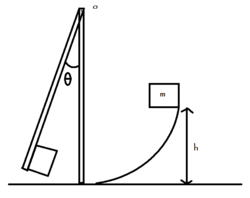 The part of mass
m
in the figure above slides down the frictionless surface through height
h
and collides with the uniform vertical rod of mass
M
and length
d
, sticking to it. The rod pivots about the point
o
through the angle
θ
before momentarily stopping. Then
θ
can be expressed as
The part of mass
m
in the figure above slides down the frictionless surface through height
h
and collides with the uniform vertical rod of mass
M
and length
d
, sticking to it. The rod pivots about the point
o
through the angle
θ
before momentarily stopping. Then
θ
can be expressed as
θ = cos − 1 [ α − d ( γ m + M ) × ( ν m + M ) β m 2 h ]
What is the value of α + β + γ + ν ?
Do you enjoy this problem? try some more .
The answer is 12.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Discussions for this problem are now closed
@Anish Puthuraya , but don't you think this is a case of inelastic collision, and there is indeed a loss of energy in it when it gets stick to the rod, how can you apply conservation of energy?
Sorry for the late reply. If you notice carefully, Ive used conservation of energy just after the collision to the peak of the oscillation. Hence, as there is no loss in energy in this process, conservation of energy is valid.
I agree that there is loss in energy during the collision (since it is inelastic), but there is no such loss after the collision.
Similar solution to Anish,but his is way better.I used calculus where it was unnecessary .
⇒ ω = ( M + 3 m ) d 3 m 2 g h
⇒ ∫ 0 θ τ d θ = 2 1 I ω 2
⇒ ∫ 0 θ X c m ( M + m ) d sin θ . d θ = 2 1 I ω 2
⇒ − cos θ + 1 = ( M + 3 m ) ( M + 2 m ) d − 6 m 2 h
⇒ α + β + γ + v = 1 + 2 + 3 + 6 = 1 2
The velocity of mass m when it is about to strike the rod is given by,
v = 2 g h
Now, it is very common to commit a mistake here. We may think that we should apply Conservation of Linear Momentum .
But, note that the Conservation of Linear Momentum is valid only when there is no external force on the system. And here, the external force is that of the reactionary force at the hinge of the rod.
Hence, we cannot apply Linear momentum conservation here. But, if we consider the net torque about the hinge of the rod, then we can see that there is no external torque on the system. Hence, it is valid to apply Conservation of Angular Momentum . We use this to relate the angular velocity before and after the collision:
L i = L f
m 2 g h d = I h i n g e w = ( m d 2 + 3 M d 2 ) w
⇒ w = ( M + 3 m ) d 3 m 2 g h
Now, to find the angular displacement of the system, we can use Conservation of Energy, from right after the collision to the peak of the swing:
K i + U i = K f + U f
2 1 I w 2 = Δ U r o d + Δ U m
M + 3 m 3 m 2 g h = M 2 d ( 1 − cos θ ) g + m d ( 1 − cos θ ) g
M + 3 m 3 m 2 g h = ( 1 − cos θ ) d ( 2 M + 2 m )
⇒ cos θ = 1 − ( M + 3 m ) ( M + 2 m ) d 6 m 2 h
⇒ θ = cos − 1 ( 1 − ( M + 3 m ) ( M + 2 m ) d 6 m 2 h )
Hence, we get,
α + β + γ + ν = 1 2