To infinity and beyond
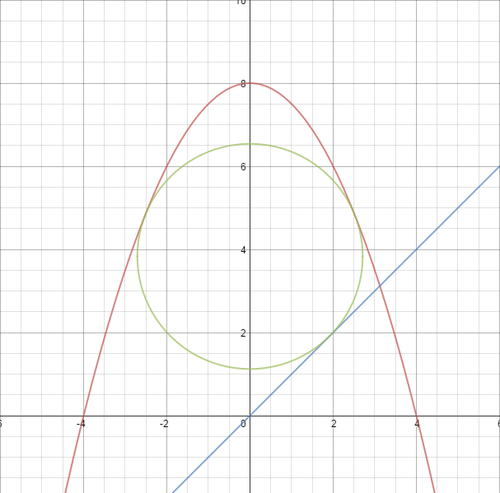If the radius of the largest circle which can be inscribed inside the region bounded by
and
can be expressed in the form
where a and b are integers and
is not divisible by the square of any prime, find
.
The answer is 55.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
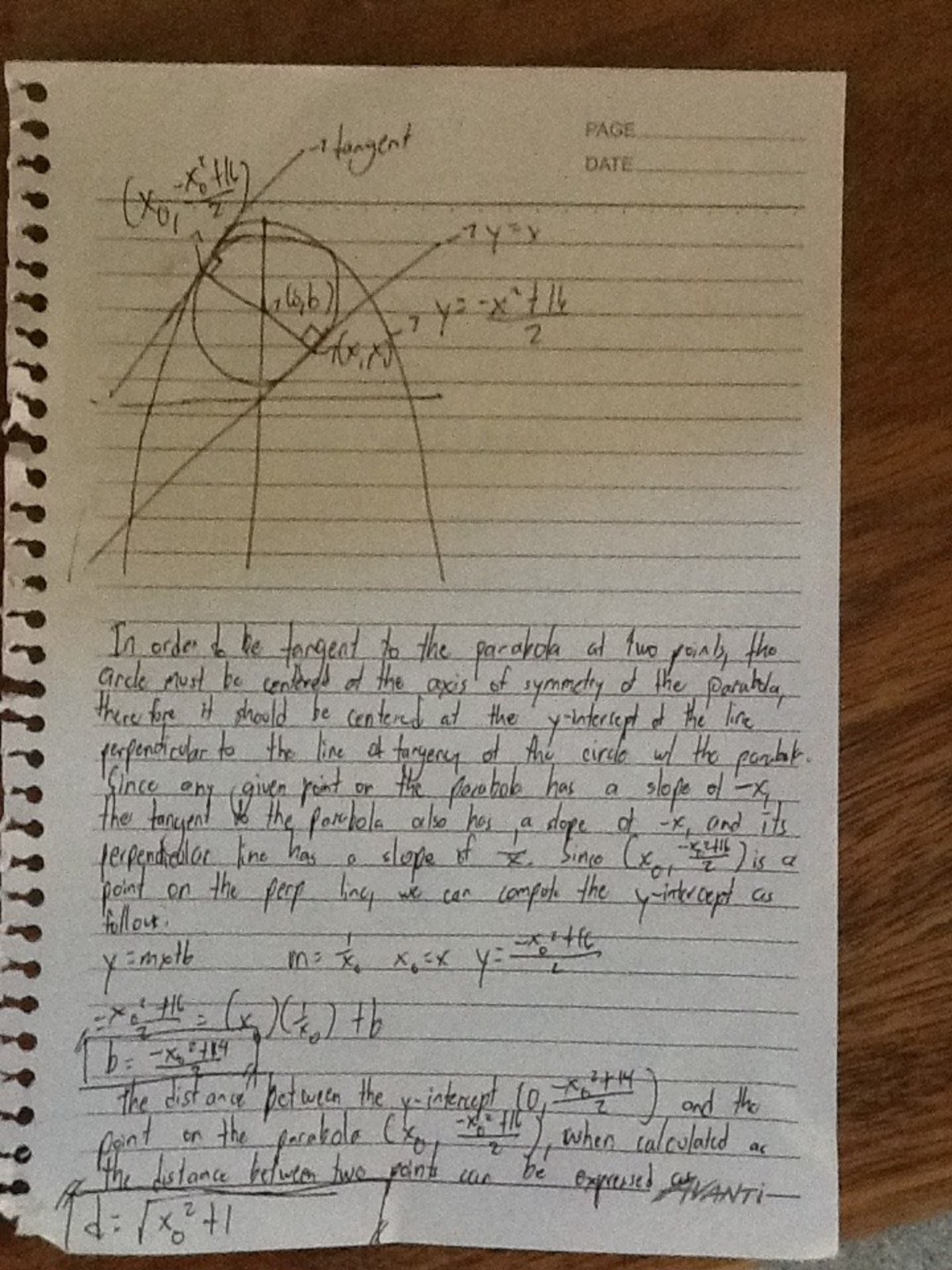
Clearly the center of the circle must be at {x=0} due to symmetry. Let the equation of the circle be x 2 + ( y − k ) 2 = r 2 . The shortest distance from the center of the circle to the line must be the radius, which is k / 2 . Plugging in the value of the radius and the equation of the parabola into the equation of the circle, we get x 2 − k 2 / 2 + ( 8 − k − x 2 / 2 ) 2 = 0 . Now we want to find the value(s) of k for which this equation has only two solutions. The discriminant with respect to x is ( k 2 − 3 2 k + 1 2 8 ) ∗ ( k 2 + 4 k − 3 0 ) 2 / 2 . Setting the discriminant equal to {0} and solving for k , we get k = 8 ( 2 − 2 ) , k = 8 ( 2 + 2 ) , k = − 2 − 3 4 , k = − 2 + 3 4 , and the only value of k that satisfies the constraints of the problem is k = − 2 + 3 4 .