Given the clues ... solve the crossword
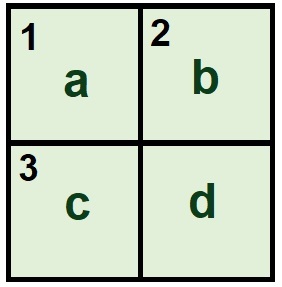
Given that a, b, c, and d are four different digits that are obtained when solving the crossword puzzle that is shown, what is the result of ?
Across:
(1) A number divisible by 5.
(3) A number divisible by 7.
Down:
(1) A number divisible by 12.
(2) A number divisible by 13.
The answer is 19.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
First, we know that b is either 5 or 0 (since is divisible by 5 ). b cannot be 0 because it would not satisfy the second down statement( b d must be divisible by 1 3 , so b must be more than 0 ), so b is equal to 5 . If b = 5 , then d = 2 ( 5 2 is divisible by 1 3 ). Then, c must be 4 ( 4 2 is divisible by 7 ). This time, a can be equal to 2 or 8 . The problem states that there is no same digits in the four variables, so a = 8 . Thus, a + b + c + d = 5 + 2 + 4 + 8 = 1 9 .