[GK2015,National I,12]Integers and derivatives
f ( x ) is a function such that f ( x ) = e x ( 2 x − 1 ) − a x + a , where a is a parameter and a < 1 . If there exists one and only one x 0 ∈ Z such that f ( x 0 ) < 0 , what is the range of a ?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
@Alice Smith , unlike Chinese, other than hyphen (-), a space is need after punctuation marks such as comma (,), period (.), exclamation mark (!), and question mark (?).
Log in to reply
well, when a happens to be 3/2e, f(-1) happens to be equal to zero so x0=-1 is not considered as a solution, thus f(x)<0 also has only one integer solution. That means a=3/2e is also a valid value for a.
Log in to reply
You are right. I will cancel the report. Thanks.
I only had to determine which answer best fit the situation.
Plot3D [ { − a x + a + e x ( 2 x − 1 ) , 0 } , { a , 2 e 3 , 1 } , { x , − 1 , 2 1 } , AxesLabel → { a , x , f } , PlotStyle → { Orange , { Opacity [ 0 . 3 ] , Blue } } , ClippingStyle → ( Opacity [ 0 . 2 ] Magenta ) ]
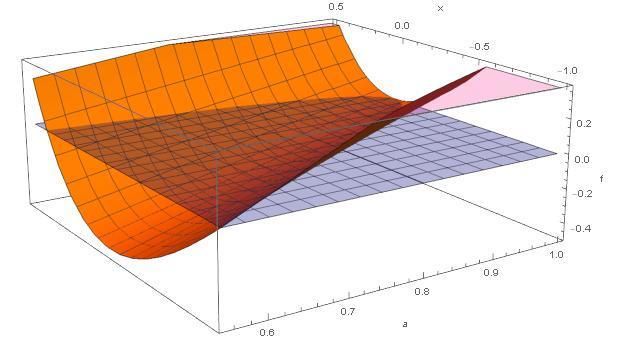
The orange surface is the function for various values of x and a. The blue plane marks the function = 0 values. The magenta areas are where the function values are outside the plot volume.
Let f ( x , a ) = e x ( 2 x − 1 ) − a x + a . Consider a = 1 , then f ( x , 1 ) = e x ( 2 x − 1 ) − x + 1 and f ′ ( x , 1 ) = e x ( 2 x − 1 ) + 2 e x − 1 . f ′ ( x , 1 ) = 0 when x = 0 . Since f ′ ′ ( 0 , 1 ) > 0 , min ( f ( x , 1 ) ) = f ( 0 , 1 ) = 0 , implying f ( x , 1 ) ≥ 0 for all x . Since if we reduce the value of a , we are shifting the curve f ( x , a ) downward, for f ( x , a ) < 0 , , a must be less than 1 or a < 1 and the integer x 0 must be 0 or x 0 = 0 .
Now consider f ( x , 0 ) = e x ( 2 x − 1 ) . We note that f ( x , 0 ) = 0 , when x → − ∞ and x = 2 1 . This means that f ( x , 0 ) < 0 for all x < 2 1 . For f ( x 0 , a ) to have only one integer solution, we need f ( − 1 , a ) ≥ 0 or e − 1 ( − 2 − 1 ) + a + a ≥ 0 ⟹ a ≥ 2 e 3 . Note that f ( 0 , 2 e 3 ) < 0 but f ( 1 , 2 e 3 ) > 0 , therefore there is only one x 0 which is 0.
Therefore, a ∈ [ 2 e 3 , 1 ) .