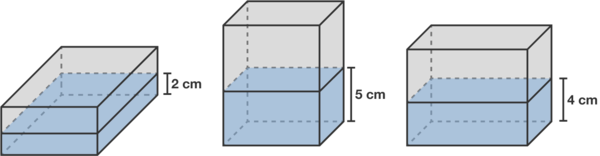
Glass Box

Call the dimensions of the box $l, w$ and $h$ . Then the volumes of the water in the three boxes are $2 \cdot l \cdot w = 5 \cdot w \cdot h = 4 \cdot l \cdot h = 160$ , so $lw = 80, wh = 32$ and $lh = 40$ . Multiplying these three equations together gives us $l^2 w^2 h^2 = 102400$ and so $V = lwh = \boxed{320}$

If the cuboid's dimensions are $a$ , $b$ and $c$ , then, the given information can be summarized in the following equations: $2ab=160$ $5bc=160$ $4ac=160$ Multiplying them we find: $(abc)^2=V^2=\frac{160^{2}\cdot 160}{40}=(160\cdot 2)^2$ $\Rightarrow V=160\cdot 2=320$

Let the dimensions of the tank be $x_1,x_2,x_3$ and the heights of the water $y_1,y_2,y_3$ . Now $\frac{y_1}{x_1} = \frac{y_1x_2x_3}{x_1x_2x_3} = \frac{V_w}{V_t} =: \alpha,\ \text{etc.},$ where $V_w$ is the volume of the water and $V_t$ is the volume of the tank. Therefore $y_1y_2y_3 = \alpha^3 x_1x_2x_3 = \alpha^3 V_t = \alpha^2 V_w.$ Thus $\alpha = \sqrt{\frac{y_1y_2y_3}{V_w}} = \sqrt{\frac{2\cdot 5\cdot 4}{160}} = \frac 12,$ showing that the tank is half-full; to finish the problem, $V_t = \frac{V_w}{\alpha} = \frac{160}{1/2} = \boxed{320}.$

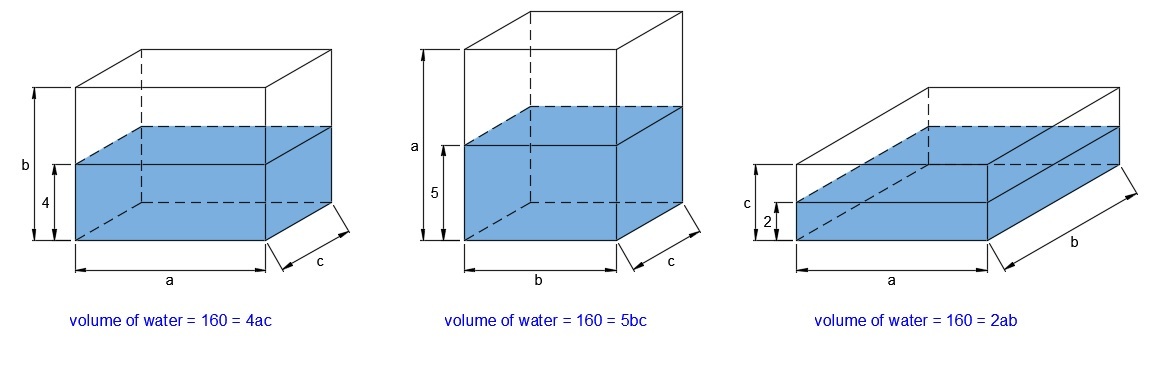
Note: The diagrams are not drawn to scale.

Consider my diagram. Let the side lengths of the rectangular prism be $a, b$ and $c$ . The volume of the cuboid is $abc$ . Since the volume of water is constant we have the three equations: $160=4ac(1),160=5bc(2)$ and $160=2ab(3)$

Multiplying the three equations, we get

$160(160)(160)=4ac(5bc)(2ab)$

$4096000 = 40a^2b^2c^2$

Dividing both sides by $40$ , we get

$102400=a^2b^2c^2$

Extracting the square root of both sides, we get

$\boxed{320} = abc$

I looked at the pictures and noticed the volume of water was half of the capacity. Chose the quick way, and doubled each volume, then multiplied the capacities of L x W x H in my head. Thanks to everyone who did it long hand. If there had been no pictures I’d have been reliant on a pen & paper

Considering the dimensions of the solid, a, b and c. The area of each face is: $a * b = 160 / 2 = 80$ $b * c = 160 / 5 = 32$ and $a * c = 160 / 4 = 40$ .

If we make $(a * b) / (a * c) = 80 / 40$ , we have $b = 2 * c$ , then replacing c in the remaining equation, $c * 2c = 32$ , so $c = 4$ . Then, $b = 2 * c = 8$ , and $a * 4 = 10$ , $a = 10$ .

The solid volume is $a * b * c = 10 * 8 *4 = 320$ .

If the volume is 160 cm^3 and the heights are 2, 4, and 5 cm, I'm looking at areas of 32, 40 and 80 cm^2. These are RECTANGLES so suddenly I'm thinking 4, 8, and 10 as the sides of a box. I hadn't even found a pencil, but 4, 8, and 10 start screaming '320!!' so I clicked it. If you can smell the answer, why engage your brain?

Let the sides of the box be x,y,z (in cm) So from the question, Volume of water = 160cm^3 = 2xy = 5xy = 4yz = 160. So, We get 3 equations, xy=80, xz=32, yz=40. => 80/y = 32/z => y=80.z/32 => 80.z^2/32 = 40 => z^2 = 16 .'. z=4 (as side length can't be a negative number)

So, volume = x.y.z = (80).4 = 320 cm^3

Look at the first picture. We know that the total volume of water is 160 and that the height is 2, so therefore, the other 2 sides, when multiplied, must give 80.

So now we know that 80 multiplied by a certain number must give us the volume.

Finally, we can deduce the total volume is 320 because that is the only multiple of 80.

Simple answer, 160 × 2 =320,thats the fastest way to the correct answer if your a Genius like me..

In logical view:: Cuboid partially(half) tank filled with water V/2 = 160 in any heights, so heights apart ,then fully filled capacity V = 160*2

I thought this is so many times more complicated. So I was complivating and complicating but at the end it was just 160•2=320 or 4•8,94427191^2=320

Another approach, shorter and faster: without pen and paper. Tank volume V is x times 160. V = 160x = (2x) (4x) (5x) as each side length of the tank is x times the water level at any of the three situations shown. Well, calculate in mind gives x=2 and V=320.

Btw,water level is perfectly scaled in the "non scaled" picture.

I guessed 320 as it is exactly twice 160.
The problem would have been better if the heights were (say) 2, 3, 6 and the possible answers rounded to nearest integer. (INT(337.31) ).
Given that most people could not do the problem without pen and paper anyway, answers which were "not neat" would be better.

The diagram was drawn to scale.

It is a trick question to make engineers do busy work. The second word and the first height is all you need to know, and it's value is arbitrary to the solution. The classification of cuboid implies all opposing sides are equal. Therefore, if it is 'X'cm on one side and you turn it over 180 degrees in any direction the cuboid requires that the height remain the same enforcing a solution of double the volume.

Take sides of cubes as 2,3,5 and take its largest multiple that is 320

Rather intuitively looking at the first figure, if you stack two such volumes of water it will equal the volume of the cuboid. It is already given one volume of such water is 160 cubic centimetre. So twice of that will be 320 cubic centimetre.

Based on the diagram, the tank looked half full to me. If the given is 160, Then double is 320.

Since the question is multiple choice, I know that one of the answers is correct. Not really how to solve the problem I guess, but how to answer the question.

Apologies to all who know what they are doing. : ) Cheers.

You can have a 3 system equation and solve by substitution:

2AB=160

5BC=160

4AC=160

Taking the 3rd equation A=(160/4C), you get:

A=40/C

Now substitute on 1st equation 2B(40/C)=160, you get:

B=2C

Then substitute in 2nd equation 5(2C)(C)=160. C=4

Now we get B in same equation 4(5)B=160, B=8

From there in 3rd equation, 4(4)A=160. A=10

ABC=320

Let's call the different dimensions of the box x,y and z.Then we have the volume of the water to be 2 x y, 4 y z and 5 x z, and x y=80, y z=40 and x*z=32. Multiplying the equations gives $x^2y^2z^2=102400$ and xyz = 320

If the level was 1 cm, then looking at the 2cm tank it would be full. So 1 cm x 2 = 320. bold text

I did the problem as stated, then I generalized it.

Below is the generalization:

Problem:

Let $a,b,c$ and $m$ be positive real numbers.

A cuboid water tank is partially filled with $\SI{m}{\centi\meter}^3$ of water. Depending on which face it rests on, the height of water in the tank is $\SI{a}{\centi\meter}, \SI{b}{\centi\meter},$ or $\SI{c}{\centi\meter}.$

What is the volume of this tank $\big($ in $\si{\centi\meter\cubed}\big)?$

$axy = m$

$bxz = m$

$cyz = m$

$\implies abcx^2y^2z^2 = m^3 \implies x^2y^2z^2 = \dfrac{m^3}{abc} \implies xyz = \sqrt{\dfrac{m^3}{abc}}$

$\therefore$ The volume $V = \sqrt{\dfrac{m^3}{abc}}$

Using $m = 160, a = 2, b = 5$ and $c = 4 \implies V = \sqrt{\dfrac{160 * 160^2}{40}} = 2 * 160 = \boxed{320}$ .

I feel so stupid looking at the very mathematical solutions here, I just looked at the diagram even though it wasn't to scale, it looked as of the water was about half of what the diagram was, so I just doubled the volume of the water.

We can easily calculate the side lengths of the water tank doubling provided hights of water accordingly. It will give us 4, 10 and 8 cm. Now we know how to calculate the tank volume: 4 $\times$ 10 $\times$ 8 = $\boxed{320}$