Global Warming and Expanding Ocean Volume
Scientist who have studied historical climate data believe that the oceans are increasing in temperature faster now that at any point in the last 10000 years. Over the last 60 years, the oceans have increased in temperature by
degrees C.
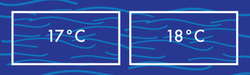
While this doesn't sound like much of a change, the density of water changes as its termperature increases. For example, water at 17 C has a density of kg/m , but water at 18 C has a density of kg/m . Assuming that in the temperature range we are considering the density function of water is roughly linear, how many more cubic km of ocean water on Earth are there now than there were 60 years ago? (give the nearest answer)
Assume that the current volume of the ocean is approximately
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Change in density/change in temperature = -0.2/1 = -0.2 Since density function is linear it should be of the form density, D = -0.2T + K ; where T is temperature To find constant K put initial values (998.8,17) or final values (998.6,18). This gives K = 1002.2 but this is not needed.
Anyway, density function is D = 1002.2 - 0.2T
Differentiate this: dD = -0.2 dT dT = 0.18 (over last 60 years)
Hence dD = -0.2*0.18 = -0.036
Now, density=mass/volume D=m/V differentiate this: dD/D = -dV/V
Hence Change in volume dV = - V dD/D = - 1.333*10^{9} * (-0.036)/ 1000 = 5 x 10^{4} (approximately)
D = 1000 kg/m^{3} is taken as density of water
Positive dV implies the volume is increasing...