Go The Distance
A semicircle is drawn on the side with length 10 of a rectangle, as shown in the diagram above.
Then a line is drawn from the point 3 units to the left of the bottom right corner, such that it is tangent to the semicircle.
Where do this line and the upper side of the rectangle intersect?
Enter the distance X , correct to 2 decimal places.
The answer is 8.33.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Elegant solution. :) (It took me a minute to realize that you applied the TTT twice to establish the X + 3 length.)
Did the same .
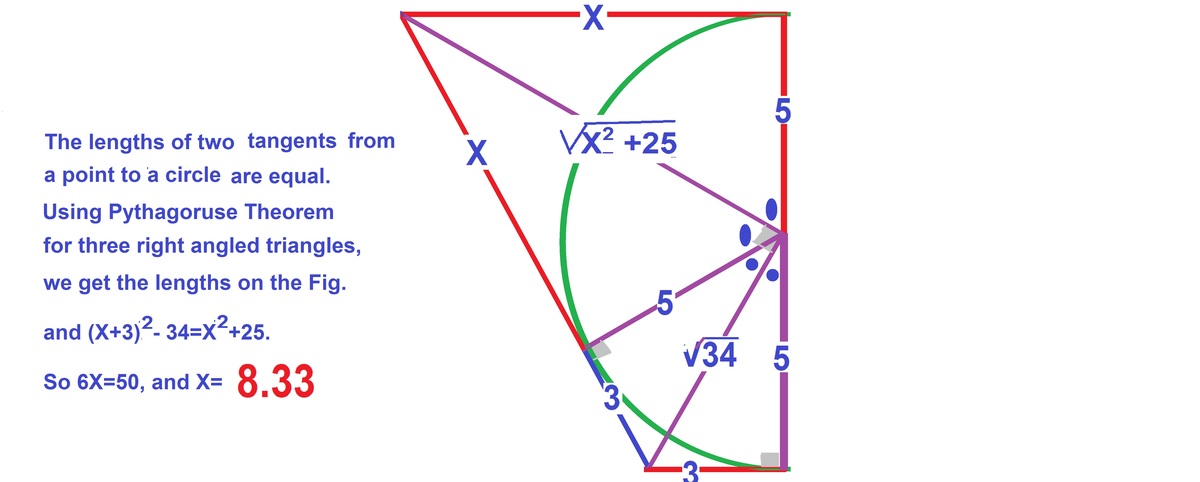
 Tangent to Semicircle in Rectangle
Tangent to Semicircle in Rectangle
The angles made by the tangent with the top and bottom edge of the rectangle are supplementary. So half of these angles α and β will be complementary.
So tan α = x 5 = cot β = 5 3 giving x = 3 2 5 = 8 . 3 3 3 3
Beautiful short solution. +1)
The line drawn starting from the point 3 units to the left of the bottom corner and tangent to the semi-circle has a length of X + 3 by the Two Tangents Theorem (Ice Cream Cone Theorem, Hat Theorem, etc.), which states that given a circle, if P is any point lying outside the circle, and if A and B are points such that PA and PB are tangent to the circle, then PA = PB.
By the Pythagorean Theorem , ( X − 3 ) 2 + 1 0 2 = ( X + 3 ) 2 . Solving for X , we get X = 8 . 3 3 .