Go to the Right, Counter!
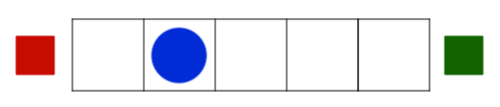 Suppose I play a game involving a counter and a
-square grid, as shown above.
Suppose I play a game involving a counter and a
-square grid, as shown above.
Assign the values
to
to the squares in the grid from left to right.
I start with the counter on square
On each turn, I roll a standard six-sided die.
If the number that is rolled is less than or equal to the number (i.e. between
and
inclusive) of the square which the counter is on, I move the counter to the left one square. Otherwise, I move the counter to the right one square.
If I move the counter onto the green square, which is shown in the picture, I win.
However, if I move the counter onto the red square, I lose.
If the probability that I win the game is represented by for positive coprime integers and what is the value of
The answer is 8.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
For integers 0 ≤ n ≤ 6 , let P n be the probability that if the counter were on square n , I win the game. (We let the green square be square 6 and the red square to be square 0 .) From the description given in the problem, if the counter were on square n , it has a 6 n chance of moving left to square n − 1 and a 6 6 − n chance of moving right to square n + 1 . If the counter moves right, then the probability that I win would then become P n + 1 , by our definition. Similarly, if the counter moves left, the probability that I win is P n − 1 . The combination of both of these probabilities gives P n , so we get
P n = ( 6 n ) P n − 1 + ( 6 6 − n ) P n + 1 .
Noticing that P 0 = 0 (I lose the game) and P 6 = 1 (I win the game), we get the system of equations
6 5 P 2 3 1 P 1 + 3 2 P 3 2 1 P 2 + 2 1 P 4 3 2 P 3 + 3 1 P 5 6 5 P 4 + 6 1 = P 1 = P 2 = P 3 = P 4 = P 5 .
Solving this for P 1 yields P 1 = 1 3 5 , so our desired answer is 1 3 − 5 = 8 .