Limits! I love' em

Calculus Level 3

lim ⁡ x → − ∞ x 4 sin ⁡ ( 1 x ) + x 2 1 + ∣ x ∣ 3 = ? \lim_{x\to-\infty } \dfrac{x^4 \sin\left( \tfrac1x\right) + x^2}{1+|x|^3} = \, ?


The answer is -1.

Arghyadeep Chatterjee by Arghyadeep Chatterjee , 22, India

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

2 solutions

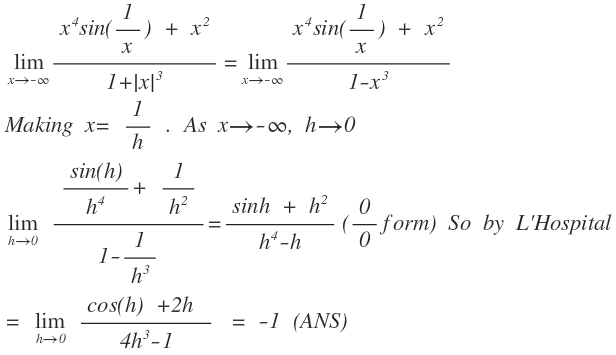
2 Helpful 0 Interesting 0 Brilliant 0 Confused

The last step of applying L'Hospital you can do it by just observing that sin h / h will become 1 and in denominator it will be -1 . I just did it because I love to use L'Hospital.

Arghyadeep Chatterjee - 3 years, 1 month ago
N. Aadhaar Murty
Mar 8, 2021

We can substitute x = − t x=-t to get rid of the absolute value -

L = lim ⁡ x t o − ∞ x 4 sin ⁡ ( 1 x ) + x 2 1 + ∣ x ∣ 3 = lim ⁡ t → ∞ − t 4 sin ⁡ ( 1 t ) + t 2 1 + t 3 L = \lim_{x\ to -\infty} \frac {x^4 \sin(\frac {1}{x})+x^2}{1 + |x|^3} = \lim_{t \to \infty} \frac {-t^4 \sin(\frac {1}{t}) + t^2}{1 + t^3}

Since we get a ∞ ∞ \frac {\infty}{\infty} form, we can use L'Hopital -

L = lim ⁡ t → ∞ − 4 t 3 sin ⁡ ( 1 t ) + t 2 cos ⁡ ( 1 t ) + 2 t 3 t 2 = lim ⁡ t → ∞ − 4 3 t sin ⁡ ( 1 t ) + cos ⁡ ( 1 t ) 3 + 2 3 t = − 4 3 ⋅ 1 + 1 3 = − 1 L =\lim_{t \to \infty} \frac {-4t^3 \sin(\frac {1}{t}) + t^2 \cos(\frac {1}{t}) + 2t}{3t^2} = \lim_{t \to \infty} \frac {-4}{3}t \sin\left(\frac {1}{t}\right) + \frac {\cos(\frac {1}{t})}{3} + \frac {2}{3t} = \frac {-4}{3} \cdot 1 + \frac {1}{3} = \boxed {-1}

0 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...