Going to the Castle - Part 5

There are two ways to reach the first ice cream shop, and there are $\binom{7}{3}$ ways to go from the first ice cream shop to the tower. To see this notice that you must take seven (block sized) steps, three of which must be to the north. So you must choose 3 out of 7 to be in the northerly direction, which can be done in $\binom{7}{3}$ ways.

Thus $2\times \binom{7}{3}$ routes take in the first ice cream shop.

Similar reasoning shows that $2\times \binom{7}{3}$ routes take in the second ice cream shop.

We cannot simply add these to get the answer, because we would then have double counted the routes taking in both shops. The number of routes taking in both shops is

$\text{ways to first shop}\times\text{ways from first to second shop}\times\text{ways from second shop to castle}$

$=2\times\binom{5}{2}\times2$

so adding everything up and correcting for the double counting the number of ways is

$4\left(\binom{7}{3}-\binom{5}{2}\right)$

$=4\left(\frac{7\times 5\times6}{3\times2}-\frac{5\times4}{2}\right)$

$=4(35-10)=\boxed{100}$

It's probably easiest to count the complement first, i.e., the number of routes that miss both ice cream shops. Label the grid so that we start at the origin $(0,0)$ and finish at $(5,4).$ Now look at the following cases that avoid both shops:

• (a) First go to $(0,2).$ Now there are two sub-cases to consider:

--- (i) travel straight through to $(5,2)$ and then up to the finish, and

--- (ii) travel to $(3,4)$ in one of $\dbinom{5}{2} = 10$ ways, and then head right to the finish:

• (b) First go to $(2,0).$ Now there are two sub-cases to consider:

--- (i) travel to $(3,4)$ in one of $\dbinom{5}{1} = 5$ ways, and then head right to the finish, and

--- (ii) travel to $(5,2)$ in one of $\dbinom{5}{2} =10$ ways and then head up to the finish.

Thus there are $1 + 10 + 5 + 10 = 26$ routes that avoid both ice cream shops. Now as there are $\dbinom{9}{4} = 126$ routes we can take without restrictions, we can conclude that there are $\boxed{100}$ routes that visit at least one of the ice cream shops.

Comment: In general, the number of routes from the lower left corner to the upper right corner of an $m$ by $n$ grid, making only unit steps north and east, is $\dfrac{(m + n)!}{m!\times n!} = \dbinom{m + n}{m}.$ The reasoning for this formula is provided here .

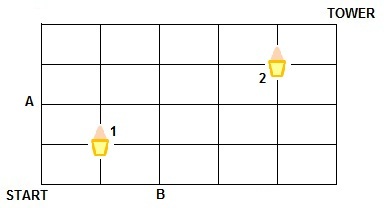
Let us first go to Cone-1 definitely. This can be done in 2 ways(NE or EN). Now the Tower is at (3N,4E) from Cone-1. The total number of ways to reach the tower from cone-1 is arrangement of 3N's & 4E's which can be done in $^{7}C_{3}$ = 35 ways.

So 2x35 = 70 ways to take Cone-1 and reach tower. This will also include the ways in which both cone-1 & cone-2 have been collected.

Now we need ways to reach only cone-2(& skip cone-1).

Path 1: Go to A, go to cone-2. Now cone-2 is at (1N,4E) from A. The total number of ways to reach cone-2 from A is arrangement of 1N's & 4E's which can be done in $^{5}C_{1}$ = 5 ways.

Path 2: Go to B, go to cone-2. Now cone-2 is at (3N,2E) from B. The total number of ways to reach cone-2 from B is arrangement of 3N's & 2E's which can be done in $^{5}C_{3}$ = 10 ways.

After following either Path 1 or Path 2, 2 ways are there from cone-2 to tower (NE or EN). Hence total 2x(5+10)=30 ways to collect only cone-2 & reach tower.

In all, 70+30 = 100 ways.

This problem is immediately simplified if you use the principle of inclusion and exclusion.

We want to count the total routes in which we get at least one ice cream.

Thus imagine the set we want is $A\cup B$ where $A$ is the paths that stop at the first ice cream cone and $B$ is the paths that stop at the second ice cream cone on the way to the Tower of London.

For our first cone we have $2 \choose 1$ $\cdot$ $7 \choose 3$ total paths that stop at the first ice cream cone that get us to the Tower of London. Conversely, we have we have $7 \choose 3$ $\cdot$ $2 \choose 1$ total paths that stop at the second ice cream cone that get us to the Tower of London. Now, we could add both resulting products together and produce a set that contains all of the ways to get to the Tower of London such that we have stopped at an ice cream cone along the way... but we would be double counting since in both products we include the number of ways to stop at both ice creams... in other words, our sum would include the intersection of sets $A$ and $B$ and we don't want this in our final result.

Therefore to view this in terms of the principle of inclusion and exclusion we subtract out the number of ways we can get to the Tower of London such that we stopped at both the first and second ice cream cone. This yields the result

$|A\cup B|=|A|+|B|-|A\cap B|=$ $|A\cup B|=\binom{2}{1}\cdot\binom{7}{3}+\binom{7}{3}\cdot\binom{2}{1}-\binom{2}{1}\cdot\binom{5}{2}\cdot\binom{2}{1}$ $|A\cup B|=100$

There are ${2}\choose{1}$ ways to go to the first ice cream shop and ${7}\choose{3}$ ways after that to go to the castle.

Consequently, there are ${2}\choose{1}$ $\times$ ${7}\choose{3}$ ways to go to the first ice cream shop and get to the castle.

By symmetry, the same goes for the number of ways to go to the second ice cream shop and get to the castle.

Now, we only have to subtract the number of ways to go to both ice cream shops and the castle.

We know there are ${2}\choose{1}$ ways to go to the first ice cream shop from the starting point and from the second ice cream shop to the castle. The number of ways to go from the first ice cream shop to the second is just ${5}\choose{2}$ .

The number is therefore $100$ :

$2$ $\times$ ${2}\choose{1}$ $\times$ ${7}\choose{3}$ $-$ ${2}\choose{1}$ $\times$ ${5}\choose{2}$ $\times$ ${2}\choose{1}$ $=$ $100$