Going with the Flow
Find the upward flux of F = y i − x j through the surface S given by x 2 + y 2 + z 2 = 4 and z ≥ x 2 + 2 y 2 .
The answer is 0.00.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Note that F = ∇ × G , where G ( r ) = 2 1 ( x 2 + y 2 ) k . Using Stokes' Theorem, it follows that I = ∬ S F ⋅ d S = ∮ C G ⋅ d r , where C is the curve defining the intersection of the sphere x 2 + y 2 + z 2 = 4 and the surface z = x 2 + 4 y 2 , oriented in such a manner that S is a positively oriented capping surface for C .
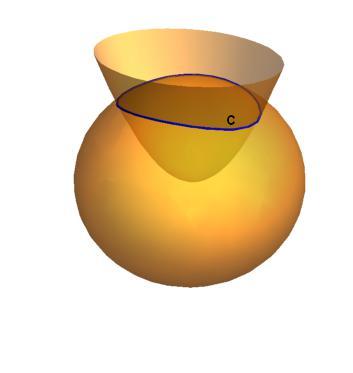
But then I = 2 1 ∮ C ( x 2 + y 2 ) d z = 2 1 ∮ C ( 4 − z 2 ) d z . If the curve C is parametrized as r = ( x ( t ) , y ( t ) , z ( t ) ) for 0 ≤ t ≤ 1 , then I = 2 1 ∫ 0 1 ( 4 − z ( t ) 2 ) z ˙ ( t ) d t = 2 1 [ 4 z ( t ) − 3 1 z ( t ) 3 ] 0 1 . Since the curve C is closed, we have z ( 0 ) = z ( 1 ) , and hence the integral I = 0 .
That's an interesting way to do this problem!
Very interesting! I did similar like you till I checked the scalar product between the normal vector and the field F. I would like to know which software you used to create this fine 3d-graphic!
The vector field F is tangent to the surface S , a part of a sphere. To verify this, take the dot product of F with the radial vector x i + y j + z k . Thus the flux is 0 .
(Recall that the flux is defined as ∫ s F ⋅ n d S , where n is the upward unit normal; the flux depends only on the component of F perpendicular to S ) . In a physical sense, the flux represents the rate at which things are flowing through the surface.