Gold hoarding groups
You have 8 identical gold coins. You are thinking about how you can group them to store in identical safety deposit boxes.
How many ways are there to group the coins? There can be any number of groups, and groups can be of any size except 0.
The answer is 22.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Is there any generalization for this?
Log in to reply
It's not really a generalization, but there's a way to use identities to solve it more efficiently. This kind of approach is helpful for creating a computer program to solve for partitions.
If p ( n ) is the partition function of n , and p ( n , r ) is the partition function of n into exactly r parts, then:
p ( n ) = k = 1 ∑ n p ( n , k )
Then, there's also the identities:
p ( n , 1 ) = 1
p(n,2)=\left\{\begin{array}{111} \dfrac{n-1}{2} & , & \text{n is odd} \\ \dfrac{n}{2} & , & \text{n is even} \\ \end{array}\right.
p ( n , n ) = 1
p(n,r)=\left\{\begin{array}{111} p(n-r) & , & n\le 2r \\ \sum\limits_{k=1}^{r}{p(n-r,k)} & , & n>2r \end{array}\right.
Now, using those identities:
p ( 8 ) p ( 8 ) = p ( 8 , 1 ) + p ( 8 , 2 ) + p ( 8 , 3 ) + p ( 8 , 4 ) + p ( 8 , 5 ) + p ( 8 , 6 ) + p ( 8 , 7 ) + p ( 8 , 8 ) = 1 + 4 + p ( 8 , 3 ) + p ( 4 ) + p ( 3 ) + p ( 2 ) + p ( 1 ) + 1
You can probably see how you can break it down even further in the next steps. There are more examples on the identical objects into identical bins page.
i have a question what was wrong with this method that I did. I took summation of (8 choose n) from 1-8. ex. (8 choose 1) + (8 choose 2)+ (8 choose 3)+ (8 choose 4)+.... (8 choose 8) and I got 255. Thanks!
Log in to reply
I think what you calculated was the number of ways to separate 8 distinct coins into only 2 groups. In this problem, note that the coins are identical . This means that it only matters how many coins are in each group; it doesn't matter which coins go in which group.
Here are a couple of ways to divide the coins into groups:
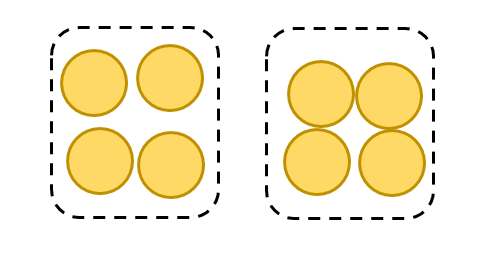 4
+
4
4
+
4
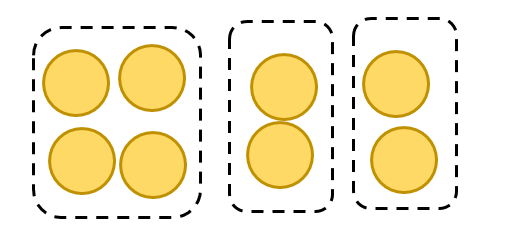 4
+
2
+
2
4
+
2
+
2
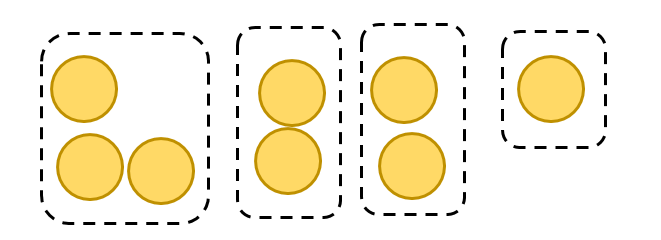 3
+
2
+
2
+
1
3
+
2
+
2
+
1
Also note that there can be any number of non-empty groups.
Another thing to keep in mind: There's an identity for what you are trying to do with the binomial coefficient:
k = 0 ∑ n ( k n ) = 2 n
Now, you left out ( 0 8 ) = 1 in that calculation, so:
k = 1 ∑ n ( k n ) = 2 n − 1
k = 1 ∑ 8 ( k 8 ) = 2 8 − 1 = 2 5 5
No generalization, manual work huh
Can you please post the generalised answer for this
Relevant wiki: Identical Objects into Identical Bins
This problem can be modeled as 8 identical objects into any number of identical bins. It is equivalent to finding the number of partitions of 8, p ( 8 ) .
These partitions are: 8 = 7 + 1 = 6 + 2 = 6 + 1 + 1 = 5 + 3 = 5 + 2 + 1 = 5 + 1 + 1 + 1 = 4 + 4 = 4 + 3 + 1 = 4 + 2 + 2 = 4 + 2 + 1 + 1 = 4 + 1 + 1 + 1 + 1 = 3 + 3 + 2 = 3 + 3 + 1 + 1 = 3 + 2 + 2 + 1 = 3 + 2 + 1 + 1 + 1 = 3 + 1 + 1 + 1 + 1 + 1 = 2 + 2 + 2 + 2 = 2 + 2 + 2 + 1 + 1 = 2 + 2 + 1 + 1 + 1 + 1 = 2 + 1 + 1 + 1 + 1 + 1 + 1 = 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1
p ( 8 ) = 2 2 , so there are 2 2 ways to group the coins.