Goldilocks And The Three Spheres
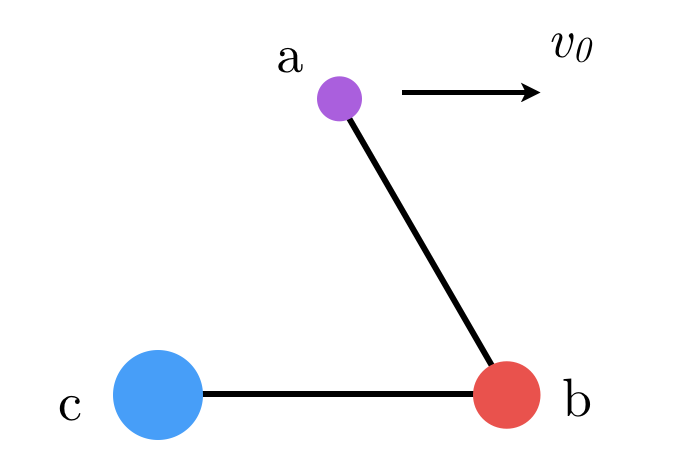
Three masses joined by elastic, inextensible strings that initially form an equilateral triangle. Mass A is given velocity parallel to side . Eventually mass C starts to move with speed , where and are co-prime positive integers.
Find .
Details and Assumptions :
- The stings are initially taut.
- The masses of A, B, and C are in the ratio .
The answer is 17.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Relevant wiki: Conservation of Momentum
The interactions between the balls occur in two stages. Initially, the string between balls A and B is taut, but goes slack as soon as A begins to move. It becomes taut again when ball A makes an angle of 6 0 ° ≡ π / 3 to the horizontal with ball B, at which point B is pulled toward A along the line connecting them. This is because a section of rope can only pull along its tangent line (can you explain why?).
Just after B is pulled toward A (at θ = 6 0 ° to v 0 ), C is pulled toward B by the taut rope connecting them (at an angle θ = 6 0 ° to the velocity of B). We have therefore argued that when balls B and C are pulled, their velocity is along the line connecting it to A or B, respectively.
Let's treat the first event. As soon as the string between A and B becomes taut, the momentum m A v 0 is reallocated between the two balls in an energy-conserving process. Thus we have (dropping the factors of 2 1 ) m A v 0 2 = m A v A 2 + m B v B 2 Momentum is conserved in each dimension. It's most convenient to treat the collision in a coordinate system ( x ′ , y ′ ) in which one dimension lies along the taut string connecting A and B. We have m A v 0 cos π / 3 m A v 0 sin π / 3 = m A v A x ′ + m B v B x ′ = m A v A y ′ We have three equations with three unknowns, thus we can solve for the velocity of ball B v B = ⟨ v B x , 0 ⟩ . Writing the energy conservation relation in components, and applying conservation of momentum in the y -dimension, we have m A v 0 2 4 1 m A v 0 2 − m B ( v B x ′ ) 2 = m A ( v A x ′ ) 2 + m A ( v A y ′ ) 2 + m B ( v B x ′ ) 2 = m A ( v A x ′ ) 2 + m B ( v B x ′ ) 2 + m A v 0 2 sin 2 π / 3 4 3 = m A ( v A x ′ ) 2 Applying momentum conservation in the x ′ -dimension, we have 4 1 m A v 0 2 − m B ( m B x ′ ) 2 = m A ( v A x ′ ) 2 = m A 1 ( 2 1 m A v 0 − m B v B x ′ ) 2 Expanding, we have 4 1 m A v 0 2 − m B ( v B x ′ ) 2 = 4 1 m A v 0 2 + m A m B 2 ( v B x ′ ) 2 − v 0 m B v B x ′ which leads to m B ( v B x ′ ) 2 ( 1 + m B / m A ) = v 0 m B v B x ′ and therefore the speed v b is given by v b = ∣ ∣ ∣ v B x ′ ∣ ∣ ∣ = m A + m B m A v 0 We argued above that the interaction between A and B is of the same nature as the one between B and C. Therefore, the initial speed of C is given by v c = m B + m C m B v b = m B + m C m B m A + m B m A v 0 In the general case of n items in an equilateral arrangement with l ( A B ) ≪ l ( B C ) , l ( B C ) ≪ l ( C D ) etc., the initial velocity of the last ball is given by v n = v 0 i = 1 ∏ n − 1 m i + m i + 1 m i