I liked this problem :) I did some weird array checking, it nicely worked out, but it takes a while (~1 min.)

1
2
3
4
5
6
7
8
9

def golomb(n):
    array=[]
    c=1
    while len(array)<n:
        array.append(c)
        if (array.count(c)==array[c-1]):
            c+=1
    return array[-1]
print golomb(123456)

Golden ratio asymptotic solution

$p=\frac {1+ \sqrt{5}}{2},\\ \\ \\ Answer = 123456^{p-1}p^{2-p}$

$1684$

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17

#include <bits/stdc++.h>
using namespace std;
int main()
{
    vector<int> v;
    v.push_back(1);
    v.push_back(2);
    v.push_back(2);
    int k=3;
    for(int i=2;i<123456;i++)
    {
        for (int j = 0; j < v[i]; ++j)v.push_back(k);
        k++;
        if(v.size()>=123456)break;
    }
    cout<<v[123455]<<endl;
}

$\boxed{1684}$

a=[1]

 for i in range(10000):

        x=int(i+1)

       for j in range(a[i]):

       a.append(x)
  a[1]=2

  print a[123456-1]

1684

The straightforward solution is to generate the sequence until we reach the $123456$ -th term.

1
2
3
4
5
6
7
8
9

n = 123456
f = [0,1,2,2]    # 0 as the dummy number

idx = 3
while len(f) <= n:
    f += f[idx] * [idx]
    idx += 1

print f[n]

To investigate further on this sequence, I found the recurrence relation from wikipedia :

$f(n) = \begin{cases} 1 & \quad n = 1\\ 1 + f(n-f(f(n-1))) & \quad n > 1\\ \end{cases}$

Here I'll give a short explanation on why this works. To compute $f(n)$ for $n>1$ , our goal is to identify $k$ such that $f(k) + 1 = f(n)$ . By definition, $f(n)$ is the number of occurrence of $n$ . Hence $f(f(n))$ is the number of occurrence of $f(n)$ .

Case 1 : $f(n-1) = f(n)$

In this case, $n-f(f(n-1)) = n - f(f(n))$ must fall in the place where its term is one less than $f(n)$ . Hence we just have to increment it by $1$ .

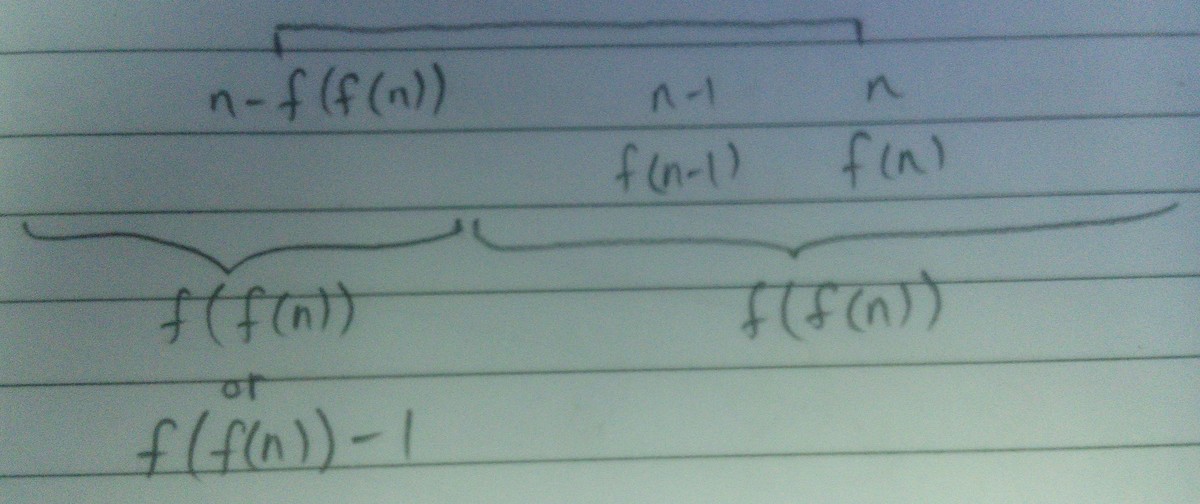
Case 2 : $f(n-1) = f(n) - 1$

In this case, the $n$ -th term is the first occurrence of $f(n)$ in the sequence. So, $n - f(f(n-1)) = n - f(f(n)-1)$ still falls in the correct place where its term is still one less than $f(n)$ .

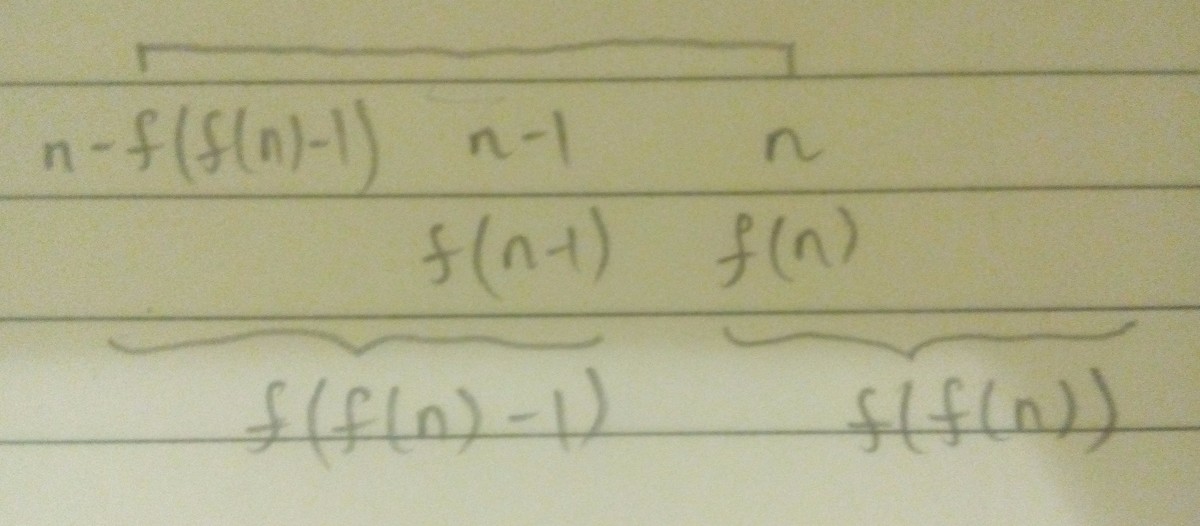
Surprisingly, this code is much slower than the naive one.

1
2
3
4
5
6
7

n = 123456
f = [0,1]

for i in range(2,n+1):
    f += [1 + f[i - f[f[i-1]]]]

print f[n]

Another approach is to consider the formula by Benoit Cloitre :

For $a_1 + a_2 + \dots + a_{n-1} < k \leq a_1 + a_2 + \dots + a_n$ we have $a_k = n$ .

With this formula, the length of sequence we have to generate is shortened because we only need to generate the sequence until the prefix sum is larger than $k$ instead of the number of terms equal to $k$ like the first one. We generate a large enough sequence and binary search for the desired $n$ .

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21

k = 123456
f = [0,1,2,2]
s = [0,1,3,5]    # prefix sum of f

idx = 3
for i in range(2000):
    f += f[idx] * [idx]
    s += [s[-1] + (i+1) * idx for i in range(f[idx])]
    idx += 1

lo = 1
hi = 2000
while lo <= hi:
    mid = (lo + hi) / 2
    if s[mid-1] < k and k <= s[mid]:
        print mid
        break
    elif s[mid-1] >= k:
        hi = mid - 1
    else:
        lo = mid + 1

Here is my code for it:

1
2
3
4
5

n = 123456
g = [1,2,2]
for i in range(3,n):
    g+=[i]*g[i-1]
print(g[-1])