Can you answer in 15 seconds? (Part 1)
2 7 − 3 x + 8 1 4 1 − x
If the expression above can be stated in the form of b x a for positive integers a and b , what is the value of a + b ?
The answer is 7.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
12 solutions
I like the way that you factored out 3 to the -x. Also, I appreciate the larger font.
I don't get it! When you add x yet you didn't add to the other 3^-x....please can you explain it to me...
Log in to reply
She didn't add x. She factored 3^-x out of both terms. When you factor it out of the first term, you end up with 1. She showed a few extra steps by showing that to 1=3^(-x+x) and therefore when you pull 3^-x out of the second term, you +x to the exponent.
Wew thanks
Please help me I don't understand THNKS
very nice thank you
good solution
Awesome question 👍🏽
How do you get from 27 to 3 ?
That's how I did it..
This is a really nice question man. The answer is so simple yet so tricky! Nice one
Why is 81 replaced with 3?
I just let x = 1 and got 1/3 + 1 = 4/3 so 4 + 3 = 7
How did you factorize it?
Brilliant question
I don't understand how you got from Step 3 to Step 4. Can someone explain?
Note that: 2 7 3 − x + 8 1 4 1 − x = 2 7 3 x 1 + 8 1 4 x − 1 1 = 3 3 ( 3 ) x 1 + 3 4 ( 4 ) ( x − 1 ) 1 = 3 x 1 + 3 x − 1 1 → 3 x 1 + 3 x 3 = 3 x 4
4 + 3 = 7
Hello MJ, You skipped a big step in adding your last set of fractions. You need to show how you added \frac{1}{3^x} to \frac{1}{3}^{x-1}.
Log in to reply
Updated :)
Mathematical artifice. That's right ..... !!!.
Okay, I get it now. You broke up the exponent of 3 to the -(x-1). You said that 3 to the -(-1) = 3 and put that into the numerator. It works.
* 2 7 ( − x / 3 ) + 8 1 ( 1 − x ) / 4 = 3 − 3 x / 3 + 3 4 4 ( 1 − x ) = 3 − x + 3 1 − x = 3 x 1 + 3 x 3 = 3 x 1 + 3 = 3 x 4 *
You made easier. That's right ..... !!!.
Note that: 2 7 3 − x + 8 1 4 1 − x = 3 3 − 3 x + 3 4 4 ( 1 − x ) = 3 − x + 3 1 − x = 3 x 1 + 3 x 3 = 3 x 1 + 3
Comparing with given form:
3 x 1 + 3 = b x a a = 1 + 3 ; b = 3
So, a+b=7
Where did the 27 and 81 go?
Log in to reply
2 7 3 − x = ( 3 3 ) 3 − x = 3 3 − 3 x
Do the same thing for the other term
After factoring we get 4/3^x as shown in other solutions. But won't seven be the minimum value of a+b since b is dependent on the value of x?
Moderator note:
Note that a and b are constants, and the answer is in terms of the variable x . So, while for different constant values of x , we could have different values of a , b , there is only 1 set that would work for all x , IE when it is the variable x .
THIS MAKES SENSE!!
2 7 − 3 x + 8 1 4 1 − x a b a + b = 3 2 7 − x + 4 8 1 − x + 1 = 3 3 3 x 1 + 4 3 4 − x + 1 = 3 x 1 + 3 − x + 1 = 3 x 1 + 3 x 3 = 3 x 4 = 4 = 3 = 4 + 3 = 7
3^3×(-x)÷3+3^4 (1-x)÷4 1/3^x+3/3^x 4/3^x 4+3 7
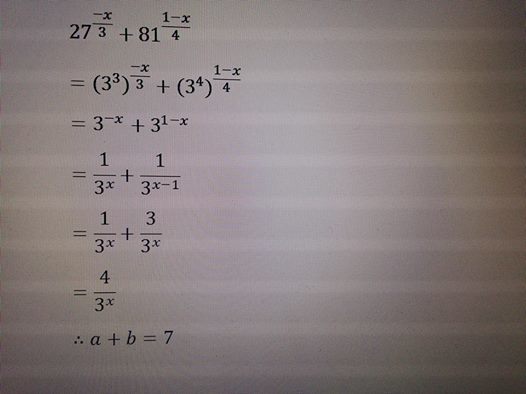
Note that:
2 7 3 − x + 8 1 4 1 − x
= 3 3 − 3 x + 3 4 4 ( 1 − x )
= 3 − x + 3 1 − x
= 3 − x ( 3 − x + x + 3 1 − x + x )
= 3 x 1 ( 3 0 + 3 1 )
= 3 x 1 ( 1 + 3 )
= 3 x 1 ( 4 )
= 3 x 4
So a + b = 4 + 3 = 7 . □