Good problem to work out...
Number Theory
Level
pending
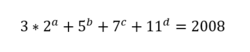If a, b, c and d are non-negative integers, find a+ b+ c + d
cannot be determined
13
7
9
11
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
The sum of left hand side equals to an even integer. We know that 2^{a} is even and other 5^{b}, 7^{c}, 11^{d} are odd. An even integer can be formed by sum of even numbers or sum of 2 odd numbers or sum of 2 odd number and a even number.
So in this problem I prefer taking sum of 2 odd nos and a even number to form 2008. so took c=0; (because maximum value 7^[c} can yield below 2008 is 343 but 5^{b} can yield upto 625 and 11^{d} upto 1331)
So intial assumption made with b=4 and d =3. Then we get 625+1331= 1956 which is 12 less than 2008 so 3* 2^{a)=12 So a=2 therfore from the assumptions a+ b+ c+ d = 9 The sum prevails same for other correct assumptions too