Counting Squares
 Let us count the number of distinct shapes that can be formed using
unit squares that are connected side to side. We consider rotations and reflections to be the same shape.
Let us count the number of distinct shapes that can be formed using
unit squares that are connected side to side. We consider rotations and reflections to be the same shape.
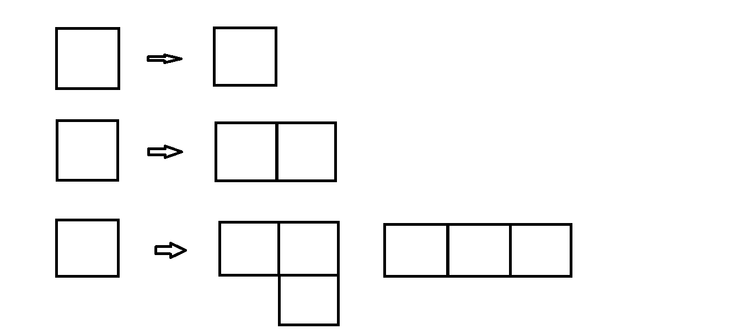
Consider the above image:
If we have 1 square, then it can only form 1 distinct shape.
If we have 2 squares, then it can only form 1 distinct shape.
If we have 3 squares, then it can form 2 distinct shapes.
If we have 4 squares, then they can form 5 distinct shapes. These are the straight line, the L-shape, the T-shape, the S-shape, and the box, which we see in a game of Tetris.
How many distinct shapes can be formed if we have 10 Squares ?
The answer is 4655.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
This doesn't seem to be a combinatorics question, but more a computer science question. How to calculate this without writing a program or just look it up via Google is beyond me. If the question asked for the number for 5 squares or even 6 squares, then it would be doable.