Good Things Come in Threes
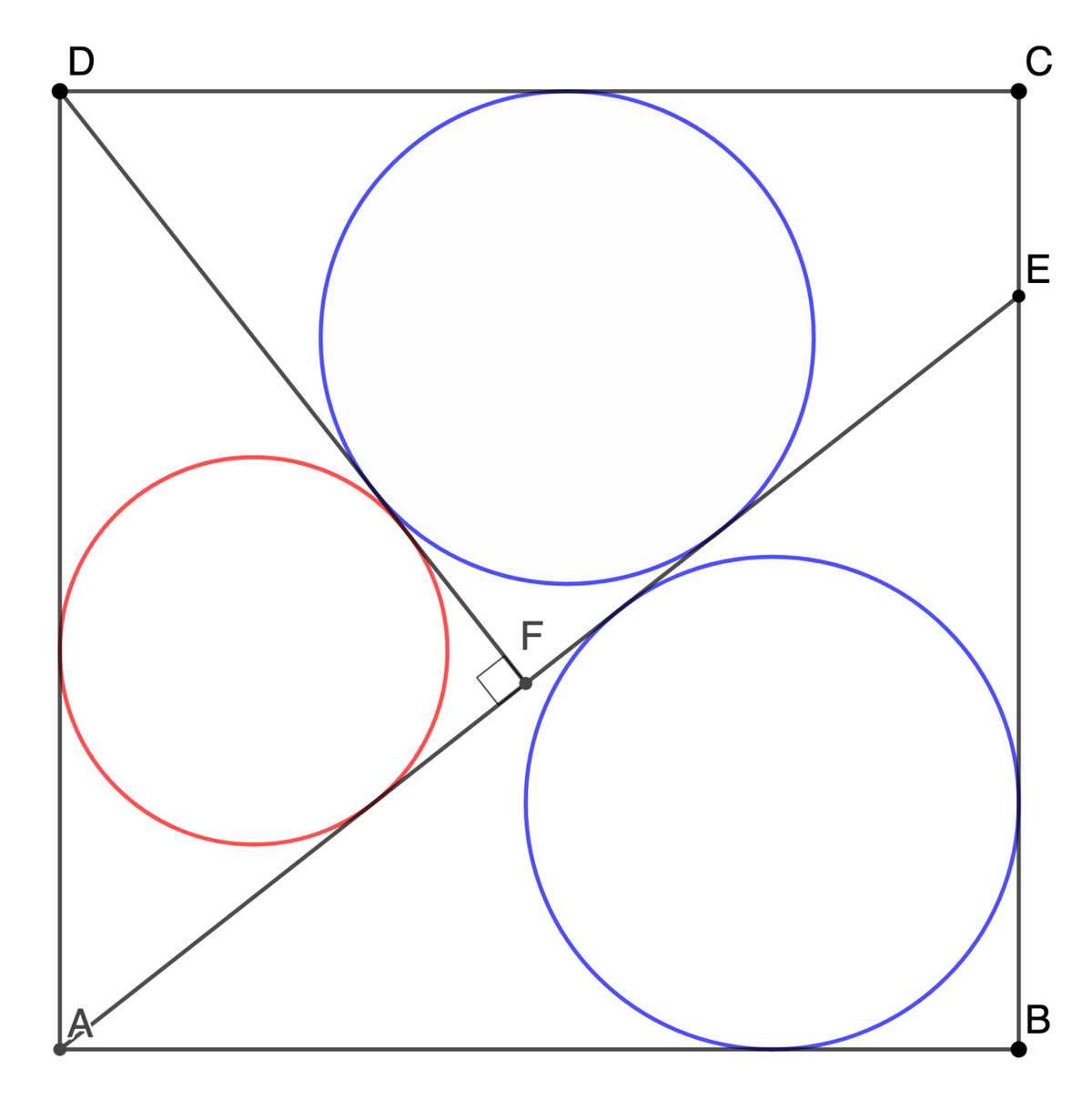
A B C D is a square. D F is perpendicular to A E . If the blue circles are congruent, what is the ratio of the radius of the blue circle to the radius of the red circle? Express the ratio as c a + b where b is square-free. Submit a + b + c .
The answer is 8.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
That's how I did it and I think it's the most elegant solution.
Let the square be in a Coordinate plane with origin at point A and A D , A B lie on y axis and x axis respectively and ∣ A B ∣ = 1 and let ∣ B E ∣ = h
Let the coordinates of point F be x 1 , y 1
Now, we know that line A B coincides with line y = h x and D F coincide with line y = 1 − h x ∴ h x 1 = 1 − h x 1 ⇒ x 1 = h 2 + 1 h ⇒ y 1 = h 2 + 1 h 2 Now, Applying distance formula ∣ D F ∣ = ( h 2 + 1 ) 2 h 2 + ( h 2 + 1 ) 2 1 = h 2 + 1 1 ∣ D F ∣ = h 2 + 1 1 Similarly, ∣ F G ∣ = h 1 + h 2 1 ∣ D G ∣ = h 1
Now, let extended D C and extended A E intersect each other at point G with coordinates x 2 , y 2
As line A B coincides with line y = h x and D C coincies with line y = 1 ∴ x 2 = h 1 , y 2 = 1
Now, as we know that inradius of right triangle with side a , b , c where hypotenuse is c = 2 a + b − c
∴ inradius of △ D F G = 2 h 1 + h 2 1 + h − 1 + h 2
∴ inradius of △ A F E = 2 1 + h − 1 + h 2
As there inradius are equal according to the question ∴ 2 h 1 + h 2 1 + h − 1 + h 2 = 2 1 + h − 1 + h 2 ⇒ h 1 + h 2 1 + h − 1 + h 2 = 1 + h − 1 + h 2 ⇒ 1 + h − 1 + h 2 = ( h 2 + h ) 1 + h 2 − ( h + h 3 ) ⇒ ( h 2 + h + 1 ) 1 + h 2 = ( h 3 + 2 h + 1 ) Squaring both the sides ⇒ ( h 2 + h + 1 ) 2 ( h 2 + 1 ) = ( h 3 + 2 h + 1 ) 2 ⇒ ( h 4 + h 2 + 1 + 2 h 3 + 2 h 2 + 2 h ) ( h 2 + 1 ) = ( 4 h 2 + h 6 + 1 + 4 h + 4 h 4 + 2 h 3 ) h 4 + h 2 + 1 + 2 h 3 + 2 h 2 + 2 h + h 6 + h 4 + h 2 + 2 h 5 + 2 h 4 + 2 h 3 = 4 h 2 + h 6 + 1 + 4 h + 4 h 4 + 2 h 3 h 4 + 1 + 2 h 3 + 2 h + h 6 + h 4 + 2 h 5 + 2 h 4 + 2 h 3 = h 6 + 1 + 4 h + 4 h 4 + 2 h 3 1 + 2 h 3 + 2 h + h 6 + 2 h 5 + 2 h 3 = h 6 + 1 + 4 h + 2 h 3 ⇒ 2 h + 2 h 5 + 2 h 3 = 4 h Dividing both sides by 2 h 1 + h 4 + h 2 = 2 ( h 2 ) 2 + h 2 − 1 = 0 From quadratic formula h 2 = 2 − 1 − + 5 as h ∈ R ∴ h 2 = 2 5 − 1 h = 2 5 − 1 Now, inradius of △ A D F = 2 1 + h 2 h + 1 − 1 + h 2 R a t i o = i n r a d i u s o f △ A D F i n r a d i u s o f △ D F G = 2 1 + h 2 h + 1 − 1 + h 2 2 h 1 + h 2 1 + h − 1 + h 2 = h 1 = 2 5 − 1 1 = 5 − 1 2 = 2 5 + 1 A n s = 5 + 2 + 1 = 8
@Fletcher Mattox how you made the construction image?
Extend A E and D C , intersecting at G : △ E B A ∼ △ D F G
As the blue circles are congruent,so △ E B A ≅ △ D F G ⟹ D F = B E △ E B A ∼ △ A F D ∴ F D A F = B A E B = A D F D ∴ F D 2 = A F × A D A F 2 + F D 2 = A D 2 A F 2 + A F × A D = A D 2 ⟹ A F = 2 5 − 1 A D F D = A F × A D = 2 5 − 1 A D r r e d r b l u e = A F B E = A F F D = 2 5 − 1 2 5 − 1 = 2 5 + 1 ⟹ a + b + c = 1 + 5 + 2 = 8
Extend D C and A E to meet at G . Then we note that △ D F G and △ A B E both have congruent incircles and same three vertex angles. The two triangles are congruent. Therefore D F = E B = x and let A B C D be a unit square. We also note that △ A D F and △ A B E are similar. Therefore,
D A D F 1 x x 2 x 4 + x 2 − 1 ⟹ x = A E A B = 1 + x 2 1 = 1 + x 2 1 = 0 = 2 5 − 1
The ratio of the radius of the blue circle to that of the red circle, r r e d r b l u e = D F A B = x 1 = 5 − 1 2 = 2 1 + 5 = φ , where φ denotes the golden ratio . Therefore a + b + c = 1 + 5 + 2 = 8 .