Google Circles 2018!
In the diagram below, 3 circles are externally tangential to one another and internally tangential to the largest, 4 circle. Three of these four circles--except for the smallest one--have their centers on a diameter of the largest circle. The second and third largest circles have radii 14 and 7, respectively.
What is the radius of the smallest circle?
The answer is 6.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
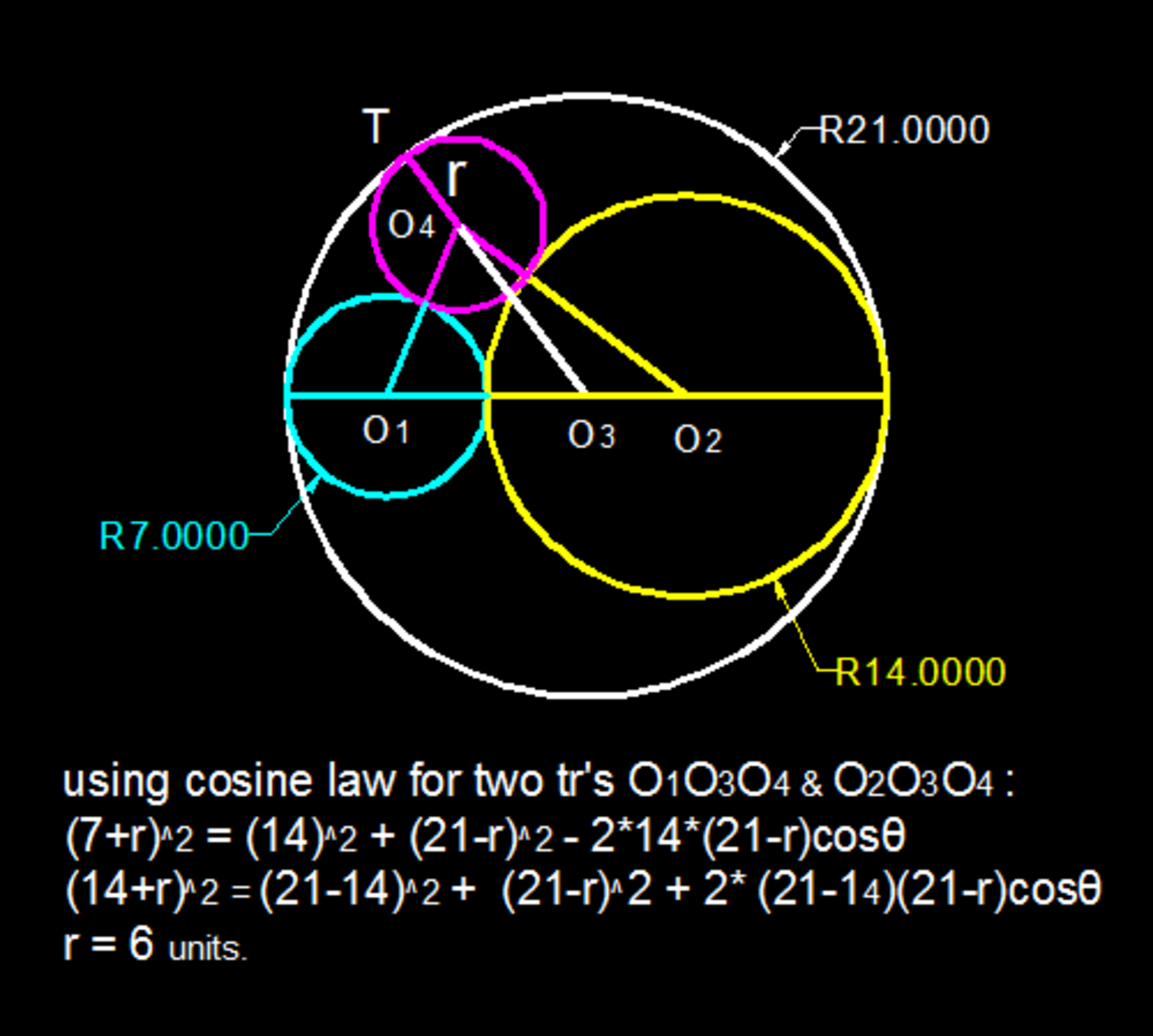
Let the radius of circle O 4 be r , the altitude O 4 P from center O 4 to the diameter of circle O 3 be h and O 1 P = a .
Because the circles are tangential to each other, the centers and the tangential point are colinear. And by Pythagorean theorem , we have:
⎩ ⎪ ⎨ ⎪ ⎧ ( 7 + r ) 2 = a 2 + h 2 ( 1 4 + r ) 2 = ( 2 1 − a ) 2 + h 2 ( 2 1 − r ) 2 = ( 1 4 − a ) 2 + h 2 . . . ( 1 ) . . . ( 2 ) . . . ( 3 )
( 2 ) − ( 1 ) : ( 1 4 + r ) 2 − ( 7 + r ) 2 1 4 7 + 1 4 r r + 3 a = ( 2 1 − a ) 2 − a 2 = 4 4 1 − 4 2 a = 2 1 . . . ( 4 )
( 3 ) − ( 2 ) : ( 2 1 − r ) 2 − ( 1 4 + r ) 2 2 4 5 − 7 0 r 5 r + a = ( 1 4 − a ) 2 − ( 2 1 − a ) 2 = − 2 4 5 + 1 4 a = 3 5 . . . ( 5 )
3 × ( 5 ) − ( 4 ) : 1 4 r ⟹ r = 8 4 = 6