Graph and discriminant
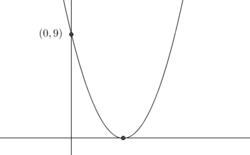 If the curve
y
=
x
2
+
b
x
+
c
touches the
x
-axis at some point and intersects the y-axis at
(
0
,
9
)
, find the
absolute value
of
b
.
If the curve
y
=
x
2
+
b
x
+
c
touches the
x
-axis at some point and intersects the y-axis at
(
0
,
9
)
, find the
absolute value
of
b
.
The answer is 6.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
7 solutions
How +6 possible X has only one soln
Since given curve touches x axis so y has some real root, say m , of multiplicity 2 . So y can be written in the form of ( x − m ) 2 , so that b turns out to be − 2 m and c turns out to be m 2 . From the second condition we can easily verify that c = 9 . Thus m 2 = 9 and hence ∣ b ∣ = 6
Vieta's Formulae tells us c/a = pq, where p and q are the roots. We have p = q, since there is only one x value making the function equal zero. Plugging in (0,9) we get c = 9 and pq = 9. Then p = q = 3. Again from Vieta, p + q = -b/a. 6 = -b. And|-6| = 6.
y = ax² + bx + c
y = x² + bx + c
Then, the value of a is 1.
(0,9) replacing the points x and y in the equation:
y = x² + bx +c.
9 = 0² + b×0 + c, then, c = 9
Looking for the parable we can see that it has 2 real and equal roots, then, ∆ = 0
∆ = b² - 4ac
0 = b² - 4 × 1 × 9
b² = 4 × 9
b² = 36
b = |√36|
b = 6
Given that (0,9) is a point on the line, we can try to figure some things out by plug this point back into y = x 2 + b x + c .
9 = 0 2 + 0 × b + c
c = 9
Now that we know what c is, our function can now be written as y = x 2 + b x + c . In the problem, we are also given that this function touches the x-axis at some point, and when a function touches the x-axis, its y-value is equal to 0. If we plug 0 in for the y-variable in y = x 2 + b x + 9 , we get the quadratic x 2 + b x + 9 = 0 . What we need to find now is the b-value.
If you consider the fact that the b-value is the sum of the factors of 9, we the following possibilities:
3 + 3 = 6
( − 3 ) + ( − 3 ) = − 6
1 + 9 = 1 0
( − 1 ) + ( − 9 ) = − 1 0
However, the only possible b-value is − 6 because 1 0 and − 1 0 's is the sum of two different factors, and there can only be one factor because there is only one root (intersection with x-axis). The reason why b = 6 is ignored is because if we plug 6 into our function, we get x 2 + 6 x + 9 = ( x + 3 ) ( x + 3 ) = 0 and solving for x would give us − 3 , which is not the right x-value if the intersection is on the positive x-axis. Thus, b = − 6 .
Finally, ∣ − 6 ∣ = 6 .
Moderator note:
After solving a problem, you should think if there is a better way of explaining the result, instead of showing every step that you took. That will help you gain a better understanding of the problem, and improve your skills over time.
The answer is -6 because b^2=4*9 the b =+-6 but taking in consideration that it touches the positive x axes it must be -6 because (b-3)^2=0 gives you a positive answer not (b+3)^2=0 if try to drow it in a grapher you will know why is it -6 not 6
x=0, y=9; then c=9; now differentiate the given equation wrt x and then equate it to zero. Find the value of b in terms of x; ie b=2x; Now put this value & y=0 in the given equation; then |x|=3; Now b=2x=6; Hence the solution.
y = x 2 + b x + c Curve passes through ( 0 , 9 ) .This point must satisfy the equation. c = 9 y = x 2 + b x + 9 Because above equation has 2 real and equal roots, then D = 0 ⇒ b 2 − 4 × 9 = 0 ⇒ b = ∣ 6 ∣