Graph Coloring- Part 1

Probability Level 3

A graph is a collection of vertices (points) joined by edges (line segments). A pair of vertices are adjacent if they are connected by an edge.

Coloring a graph refers to assigning colors to its vertices. A graph is said to be properly colored if every pair of adjacent vertices receive different colors.

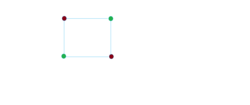
Consider the above graph with 4 vertices and 4 edges. This graph is denoted as $C_{4}$ . If you are permitted to use 6 different colors, how many proper coloring does $C_{4}$ have ?

Note:
1. Vertices are adjacent if they are joined by an edge (line).
2.The coloring that is in the figure is an example of proper coloring.

The answer is 630.

2 solutions

Tarani Meher
Mar 26, 2014

Let's name the vertices as A,B,C and D clockwise from top left. Since we are using 6 colors, we can color A in 6 ways. Since A and B are adjacent, B can be colored in 5 ways.

Now C can be given the same color as A or a different one.

If C is given the same color as A , D can be colored in 5 ways. Totally $6 \times 5 \times 5$ =150 ways.

If C is given different color, which can be done in 4 ways, D can be colored in 4 ways.Totally $6 \times 5 \times 4 \times 4$ =480 ways.

All in total 150+480=630 ways.

I did it in a much longer and more pointless way than that and now I feel sad and tired.

Duncan Schaafsma - 3 years, 9 months ago

I have now found a branch of mathematics that is beyond my comprehension and reasoning......Can anybody explain this in simple terms ?

Simon Cochrane - 4 years, 4 months ago

In general, there are (k-1)^n+(-1)^n(k-1) ways, where k is the number of colours.

Joe Mansley - 2 years, 5 months ago

What is the error in thinking that A can be chosen 6 ways, B and C in 5 ways, and D in 5 ways?

Kermit Rose - 2 years, 4 months ago

You can't necessarily colour D in 5 ways. It is adjacent to both A and C, so if A and C have the same colours, then sure you can colour D in 5 ways, but if they have different colours, then there are only 4 colours you could colour D with.

Joe Mansley - 2 years, 4 months ago

Farhad Hasankhani
Mar 10, 2016

There are three types of proper colouring(n=x+y+z): (1) Those with the property that non-adjacent vertices have the same color. To count number of these kind of colourings, note that we have 6 colour to choose for the first pair of vertices and for each of these coloring we have 5 different ways to choose colour of the second pair: so x=(6).(5)=30, (2) Those with the property that only one pair among non-adjacent vertices has the same colour. We can choose the pair that has this property in 2 ways. Then for each way there are 6 different ways to colour the pair. And for each of the ways we can colour the other two vertices in 5*4 different ways. Hence, y=(2).(6).(5).(4)=240, (3) Those with the property that all the vertices have different colours. Simply number of such coloring ways is : z=(6).(5).(4).(3)=360. Therefore, n=x+y+z=630.

Graph Coloring- Part 1

The answer is 630.

2 solutions

0 pending reports