Graph minus!
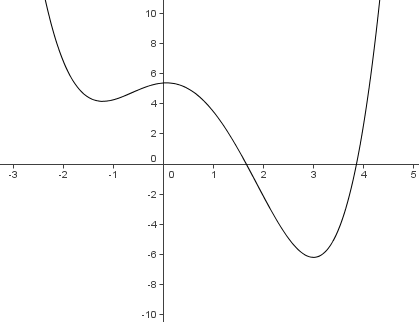
The graph above shows a portion of the curve defined by the quartic polynomial, . Which of the following is smallest?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Since P is graphed, I assume it is real, and so are a, b, c, d. A polynomial P(x) = x^4 + ax^3 + bx^2 + cx + d can also be expressed as P(x)=(x-s)(x-t)(x-u)(x-v). The intersections with the x-axis give the real zeros which we will say are at x=s and x=t.
Values are read from the graph, so I try to provide readings with estimated uncertainties.