Graphometry

Geometry Level 1

$\large \begin{cases}{y=\sin (x)} \\ {y=\cos (x)} \\ {y=\tan (x)} \\ {y=\csc (x)}\end{cases}$

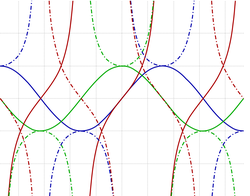
The four graphs above are drawn on the same axes from $x = 0$ to $x = \frac \pi2$ .

If a vertical line is drawn where the graphs of $y=\cos (x)$ and $y = \tan (x)$ intersect, this line intersects the graphs of $y=\sin(x)$ and $y=\csc(x)$ at points $A$ and $B$ . What is the distance between $A$ and $B$ ?

The answer is 1.

3 solutions

Jonathan Salim
May 25, 2015

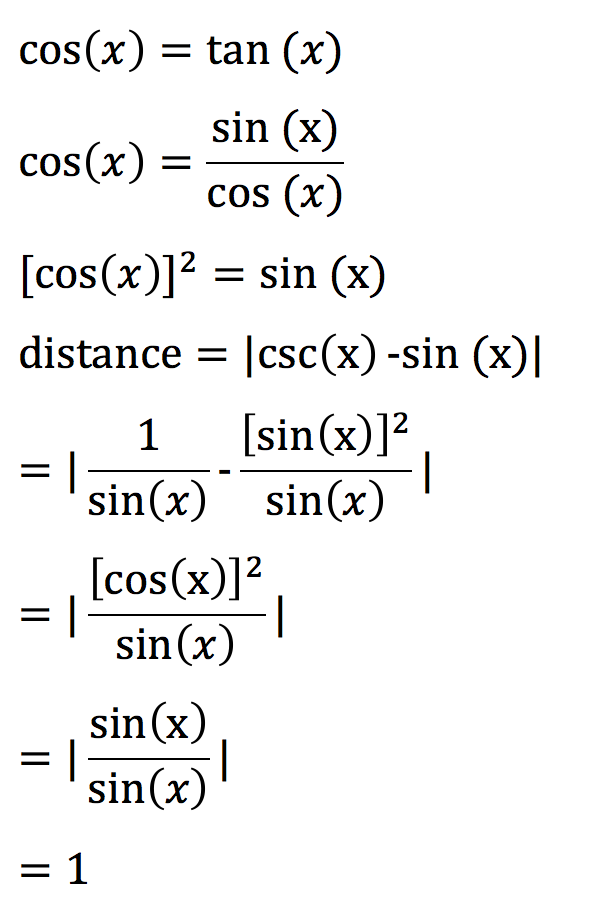
why did you take the distance as cosec(x)-sin(x)

avn bha - 6 years ago

I think the distance is |csc(x) -sin(x)| since the x values from both graph is the same since the distance can be calculated by sqrt((y1-y2)^2)

Jonathan Salim - 6 years ago

Sorry for the big font, I insert an image from ms word and suddenly it become big

Jonathan Salim - 6 years ago

Chew-Seong Cheong
May 24, 2015

When $y = \cos{x}$ meets $y = \tan{x}$

$\begin{aligned} \Rightarrow \cos{x} & = \tan{x} \\ \cos{x} & = \frac{\sin{x}}{\cos{x}} \\ \cos^2{x} & = \sin{x} \\ 1- \sin^2{x} & = \sin{x} \\ \sin^2{x} + \sin{x} -1 & = 0 \\ \Rightarrow \sin{x} & = \frac{-1\pm \sqrt{5}}{2} \\ & = \frac {\sqrt{5}-1}{2} \text{ for } x \in \left[0, \frac{\pi}{2} \right] \end{aligned}$

For $x = \sin^{-1} {\left(\frac{\sqrt{5}-1}{2}\right)}$

$\Rightarrow A = \sin{x} = \dfrac {\sqrt{5}-1}{2} \quad \Rightarrow B = \csc{x} = \dfrac{1}{\sin{x}} = \dfrac {2}{\sqrt{5}-1}$

The distance between $A$ and $B$ ,

$\begin{aligned} |A-B| & = \left| \dfrac {\sqrt{5}-1}{2} - \dfrac {2}{\sqrt{5}-1} \right| = \left| \dfrac {\sqrt{5}-1}{2} - \dfrac {2(\sqrt{5}+1)}{4} \right| \\ & = \left| \dfrac {\sqrt{5}-1-\sqrt{5}-1}{2} \right| = \left| \dfrac {-2}{2} \right| = \boxed{1} \end{aligned}$

Moderator note:

Is there another approach in which we do not need to explicitly evaluate $\sin x$ ?

Hint: For the given value of $x$ , what is $\sin ^2 x - 1$ equal to?

Why is the x = sin^-1(( root5 -1)/2) part needed?

Adolphout H - 10 months, 2 weeks ago

Because $x$ has two values $\dfrac {\sqrt 5 -1}2$ and $\dfrac {-\sqrt 5 -1}2$ and I was referring the former value.

Chew-Seong Cheong - 10 months, 2 weeks ago

Jesse Nieminen
May 27, 2015

0 <= x <= pi/2

cos(x) = tan(x)

cos(x)^2 = sin(x)

1 - sin(x)^2 = sin(x)

sin(x)^2 + sin(x) - 1 = 0

-1 <= sin(x) <= 1

sin(x) = (-1 +- sqrt(5))/2

sin(x) =(-1 - sqrt(5))/2 < -1 not accepted

sin(x) =(-1 + sqrt(5))/2

csc(x) = 1/sin(x)

|sin(x) - 1/sin(x)| = |(-1 + sqrt(5))/2 - 2/(-1 + sqrt(5))| = 1

Graphometry

The answer is 1.

3 solutions

Moderator note:

0 pending reports