Gratuitously Polarized (Part 2)

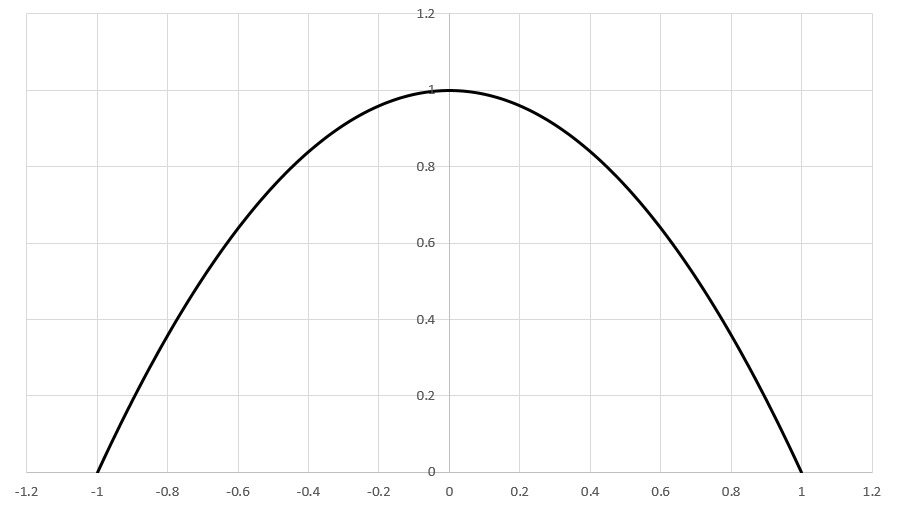
Consider the function $y = 1 - x^2$ , graphed in the range $-1 \leq x \leq 1$ . Suppose we represented the function in polar coordinates $(r,\theta)$ instead of Cartesian coordinates $(x,y)$ . Here, $r$ is the distance from the origin, and $\theta$ is the angle with respect to the positive $x$ axis.

Then we could calculate the angle-weighted average of the radius. In the expression below, the parenthetical indicates that the radius is a function of the angle.

$\large{r_{av} = \frac{\int_0^{\pi} \, r (\theta) \, d \theta}{\pi}}$

What is $\lfloor 100 \, r_{av} \rfloor$ , where $\lfloor \cdot \rfloor$ denotes the floor function?

Note: I posted Part 1 so long ago that I can't even find it anymore, except in the recesses of my own memory