Gravitationally Equivalent Point Mass
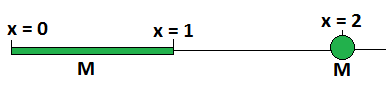
There are two objects, a thin rod of mass in the interval on the -axis, and a point mass at of the same mass , as shown above.
Suppose we wanted to replace the rod with a particle of mass , which would exert the same gravitational force on the point particle at .
What should its approximate -coordinate be?
Inspired by Steven Chase
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
We want to shrink the rod to a point such that the gravitational field at x = 2 is the same as before.
Our first instinct might be to shrink it at the point x = 0 . 5 . However, this is wrong because the parts of the rod closer to x = 2 contribute (quadratically) more to the field than the parts of the rod away from it. This is why the point mass should be closer to x = 2 than x = 0 . 5 .
To see this rigorously, we want to pick a point x such that ( 2 − x ) 2 M = ∫ 0 1 ( 2 − l ) 2 M d l
The integral can be easily solved: ∫ 0 1 ( 2 − l ) 2 M d l = ∫ 2 1 y 2 − M d y = 2 M
So, now that we have ( 2 − x ) 2 M = 2 M ⟹ ( 2 − x ) 2 = 2 , it can be clearly seen that x > 2 1