Gravity Field Strength
Help the poor editor! The illustration captions have gotten scrambled.
All the illustrations use a object radius of 1 and are normalized to a surface field strength of 1 .
The captions:
A. A radius 1 shell.
B. Uniform density
C. A uniform decline in density from 1 at the surface to 0 at the center.
D. A uniform increase in density from 0 at the surface to 1 at the center.
E. An exponential increase in density from the surface to the center, specifically e − 1 e r .
The illustrations.
Assemble the illustration numbers (left to right) in caption order (top to bottom). The resulting five digit number is your answer.
The answer is 45123.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
I did the hard computations generating the illustrations. The answer is qualitative.
A. A radius 1 shell. Quoting from Shell theorem :
Isaac Newton proved the shell theorem[1] and stated that:
-
A spherically symmetric body affects external objects gravitationally as though all of its mass were concentrated at a point at its centre.
-
If the body is a spherically symmetric shell (i.e., a hollow ball), no net gravitational force is exerted by the shell on any object inside, regardless of the object's location within the shell.
B. Uniform density. Quoting from Shell theorem :
A corollary is that inside a solid sphere of constant density, the gravitational force within the object varies linearly with distance from the center, becoming zero by symmetry at the center of mass. This can be seen as follows: take a point within such a sphere, at a distance r r from the centre of the sphere. Then you can ignore all the shells of greater radius, according to the shell theorem. So, the remaining mass m is proportional to r 3 (because it is based on volume), and the gravitational force exerted on it is proportional to r 2 m (the inverse square law), so the overall gravitational effect is proportional to r 2 r 3 = r , so is linear in r .
C. A uniform decline in density from 1 at the surface to 0 at the center.
The plot has to be pointy at the ∣ r ∣ = 1 and curved near r = 0 .
D. A uniform increase in density from 0 at the surface to 1 at the center.
The plot has to be curved at the ∣ r ∣ = 1 and straightens near r = 0 .
E. An exponential increase in density from the surface to the center, specifically e − 1 e 1 − r .
Has to resemble B with some curving like D.
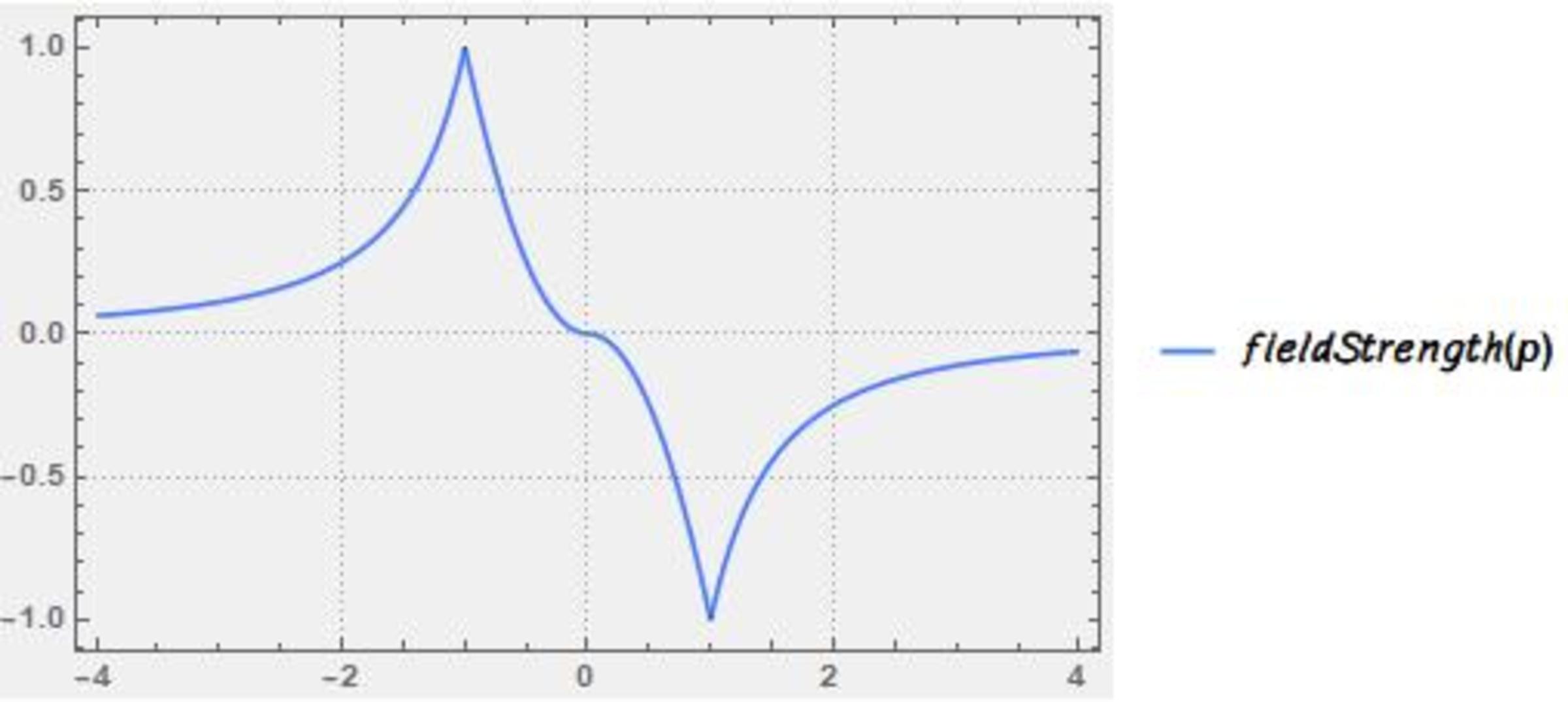
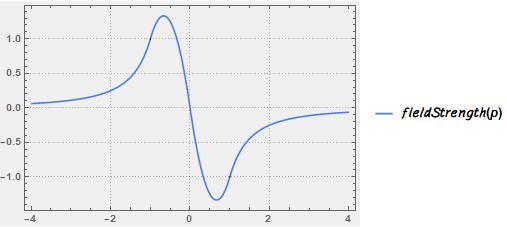
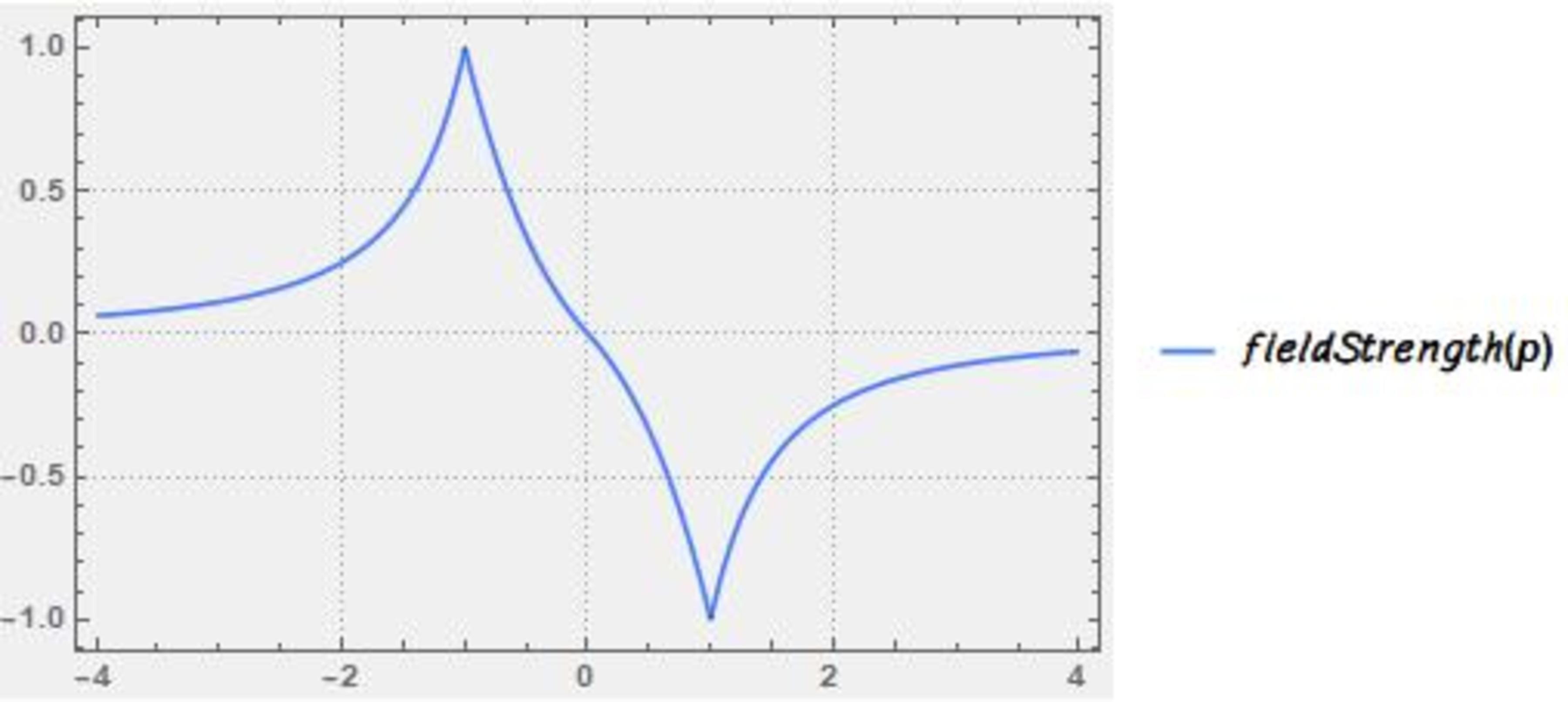
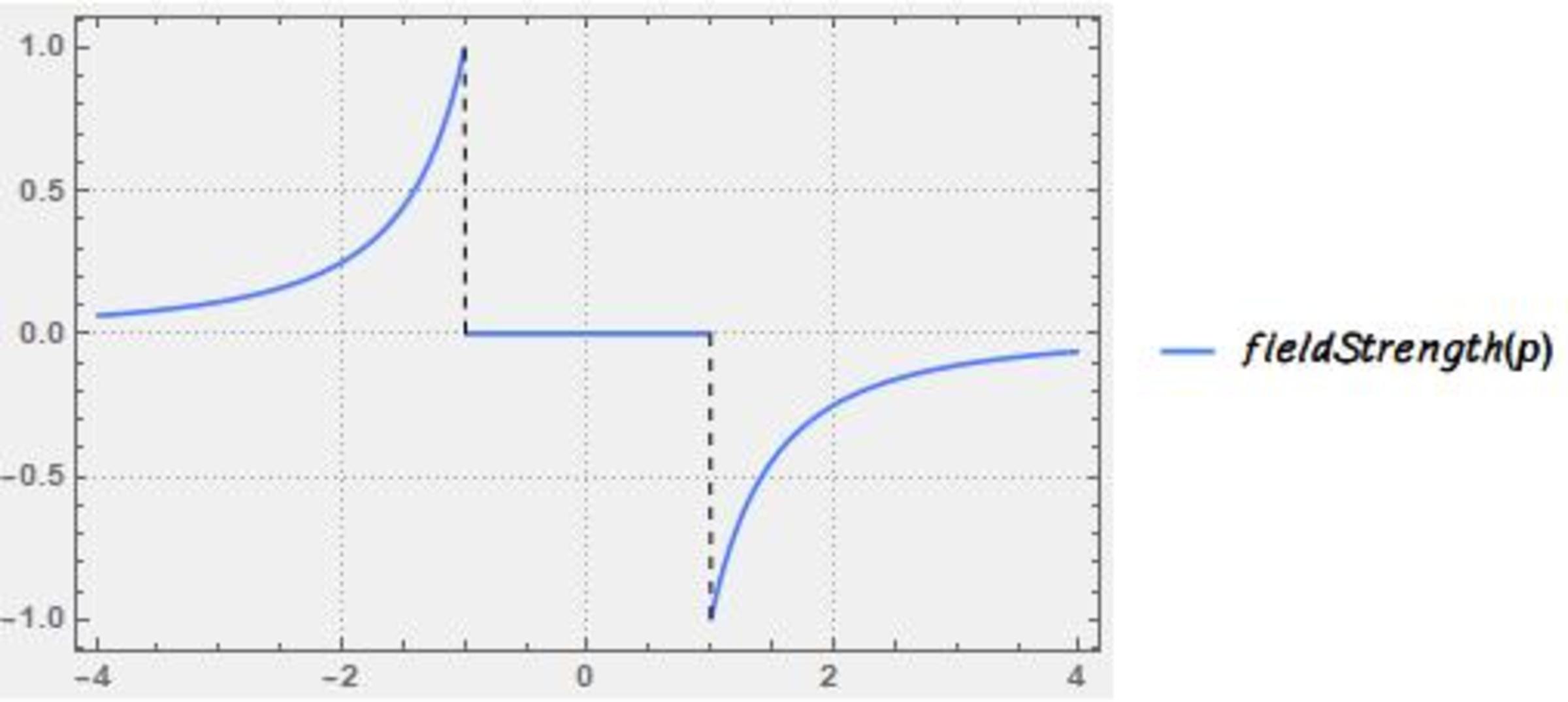
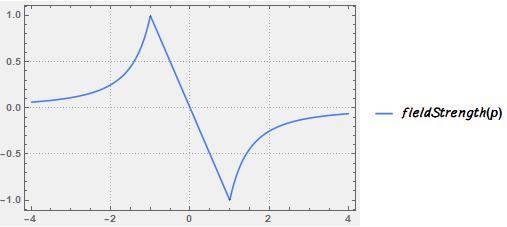
We know that E ( r ) = − r 2 1 ∫ 0 r ρ ( r ) r 2 d r . Looking for clues, we will restrict our attention to 0 < r < 1 . Except in the case of the exponential function, these field strengths are quite easy to compute.
A. A radius 1 shell: E ( r ) = 0 since the density is 0: Graph 4
B. Uniform density: E ( r ) is linear : Graph 5
C. Decline from 1 to 0, ρ ( r ) = r : The graph of E ( r ) will be a parabola with its vertex at r = 0 : Graph 1
D. Increase from 0 to 1, ρ ( r ) = 1 − r : The graph of E ( r ) will be a parabola with its vertex at r = 3 2 . Another clue: The graph of E ( r ) is differentiable at r = 1 since the density is continuous there: Graph 2
E: Exponential: Graph 3 by the process of elimination
The answer is 4 5 1 2 3
A charming problem! Thank you! Happy New Year to you!